Python Programmieren Lernen – Der vollständige Einstiegskurs
Grundlagen der Sprache
Lektion 1: Einführung in die Programmiersprache Python
Inhaltsübersicht:
Was ist Python?
Python ist eine höherwertige, interpretierte Programmiersprache, die 1986 von Guido van Rossum entwickelt wurde. Seit 1991 wird sie öffentlich genutzt.
Heute ist Python eine der beliebtesten und vielseitigsten Sprachen weltweit – für Web, Desktop, Automation, Spiele, Data Science und IT-Security.
- Desktop-Anwendungen
- Webentwicklung
- Automatisierung (Scripting)
- Spieleentwicklung
- Data Science & Machine Learning
- IT-Sicherheit und Penetration Testing
Gut zu wissen: Python funktioniert auf Windows, macOS, Linux & Co.
Vorteile von Python für Entwickler:innen
- Einfache Syntax: Lesbar & ideal für Einsteiger
- Große Community: Viele Ressourcen & Bibliotheken
- Plattformunabhängig: Lauffähig auf vielen Systemen
- Gefragte Sprache: Hohe Nachfrage am Arbeitsmarkt
- Vielfältiger Einsatz: Von Einsteiger- bis Profiprojekten
Was unterscheidet Python von anderen Programmiersprachen?
Kostenlos & Open Source
- Gratis nutzbar, auch für kommerzielle Projekte
- Quellcode ist offen einsehbar und anpassbar
Technische Vorteile
- Läuft auch auf schwächeren Geräten
- OOP mit Klassen, Vererbung etc.
- Multithreading möglich
- Anbindung an Datenbanken
- GUIs möglich
- Kompatibel mit C, C++, Java
Bildung & Lehre
- Weltweiter Einsatz in Schulen & Universitäten
Für wen ist dieser Kurs geeignet?
Dieser Kurs richtet sich an:
- Einsteiger ohne Vorkenntnisse
- Schüler, Studierende, Auszubildende
- Softwareentwickler:innen, die Neues lernen möchten
Egal ob neugierig, beim Umstieg oder zur Weiterbildung – dieser Kurs bringt dir alles bei.
Bin ich bereit, mit Python zu starten?
Wenn du noch keine Programmiererfahrung hast, empfehlen wir eine Einführung in die Programmierlogik:
- Wie denkt ein Programmierer?
- Was ist ein Algorithmus?
- Wie löst man Probleme strukturiert?
Was erwartet dich im nächsten Kapitel?
Du wirst lernen:
- Wie du Python installierst
- Welche Werkzeuge du brauchst
- Wie du dein erstes einfaches Programm startest
Lektion 2: Einrichtung der Entwicklungsumgebung
Inhaltsübersicht:
Funktionsweise eines Python-Programms
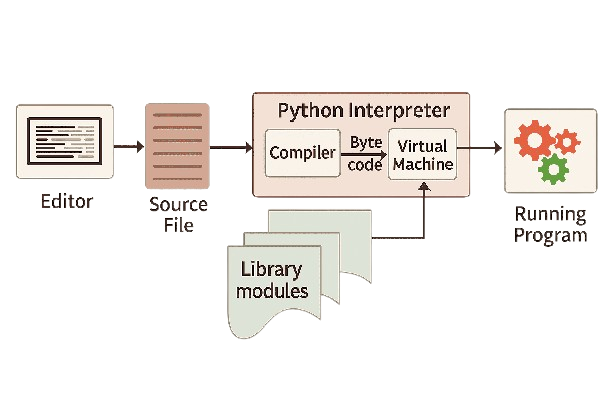
Grundsätzlich erstellen wir eine Datei mit der Endung .py, in die wir unsere Python-Befehle schreiben. Nach dem Speichern wird der Python-Interpreter gestartet, der die Befehle Zeile für Zeile ausführt.
Der von dir geschriebene Code heißt Source Code. Um diesen Code auszuführen, wird er an den Python-Interpreter übergeben. Dieser besteht aus zwei zentralen Komponenten:
- Compiler: Wandelt den Source Code in sogenannten Byte Code um (Dateiendung:
.pyc). - Virtual Machine: Führt den Byte Code auf dem Betriebssystem aus (Windows, Linux, macOS).
Technische Begriffe
- Source Code: Der Originalcode, den du schreibst.
- Byte Code: Vom Compiler erstellter Code, den die Maschine versteht (binär: 0 und 1).
- Compiler: Programm zur Umwandlung von Python-Code in Byte Code.
- Virtual Machine: Führt den Byte Code wie ein normales Programm aus.
- OS (Operating System): Das Betriebssystem – z. B. Windows, Linux, macOS.
Entwicklungsumgebung einrichten
Für diesen Kurs verwenden wir die neueste Version von Python sowie PyCharm – eine kostenfreie und benutzerfreundliche IDE, mit der du deine Projekte effizient verwalten und ausführen kannst.
- Warum PyCharm? Einfach zu bedienen, unterstützt Autovervollständigung und ist perfekt für Einsteiger.
- Alternativ kannst du auch einfache Texteditoren wie Visual Studio Code, Atom oder Notepad++ verwenden.
Tipp: In jeder neuen Programmier-Session sollte ein Projekt in der IDE erstellt werden.
Dein erstes Python-Programm
Im folgenden Beispiel erstellen wir ein einfaches Python-Programm, das die Phrase Hello World! ausgibt.
Test.py
print("Hello World!")
Ausgabe:Hello World!
In den kommenden Kapiteln wirst du kleine und verständliche Einheiten kennenlernen, die dir die Grundprinzipien von Python näherbringen. Sobald du alle Konzepte verstanden hast, wirst du in der Lage sein, komplette Anwendungen mit grafischer Benutzeroberfläche zu entwickeln.
Lektion 3: Stil und Struktur beim Schreiben von Python-Code
Inhaltsübersicht:
Groß- und Kleinschreibung
In Python ist die Groß- und Kleinschreibung entscheidend. note und Note sind zwei verschiedene Variablen:
Note = 10
print(note) # Ausgabe: 5
print(Note) # Ausgabe: 10
Benennungsregeln für Variablen, Funktionen und Klassen
Benennungen in Python folgen klaren Konventionen:
- Variablen: Kleinbuchstaben, evtl. mit Unterstrichen
- Funktionen: Wie Variablen (z. B.
calculate_sum) - Klassen: Großschreibung (CamelCase, z. B.
DataModel)
total_points = 250
def calculate_average():
pass
class User:
pass
Kommentare – Klarheit im Code
Kommentare machen deinen Code verständlich:
def average(a, b):
return (a + b) / 2
Mehrere Anweisungen in einer Zeile?
Vermeide es, mehrere Anweisungen auf eine Zeile zu schreiben – auch wenn es erlaubt ist:
Mehrzeilige Anweisungen sauber schreiben
Nutze Backslashes \ oder runde Klammern:
item_2 + \
item_3
colors = [
‚Red‘,
‚Green‘,
‚Blue‘
]
Gültige Namen verwenden
Variablennamen dürfen mit Buchstaben oder Unterstrich beginnen, nicht mit Zahlen oder Sonderzeichen:
- ✅
_name,user1,Test - ❌
1name,-value,@user
Reservierte Wörter (Schlüsselwörter)
Diese Wörter sind Teil der Python-Syntax und dürfen nicht als Namen verwendet werden:
False, finally, for, from, global, if, import, in, is, lambda, None,
nonlocal, not, or, pass, raise, return, True, try, while, with, yield
Einrückung ist Pflicht!
Python verwendet Einrückung statt geschweifter Klammern:
print(„Bestanden!“)
else:
print(„Nicht bestanden.“)
Formatierungstipps für sauberen Code
- Immer 4 Leerzeichen zur Einrückung
- Keine Tabs verwenden
- Max. 79 Zeichen pro Zeile
- Zwischen Funktionen/Klassen Leerzeilen lassen
- Kommentare klar und prägnant schreiben
Tabs in Leerzeichen umwandeln (z. B. in PyCharm)
Strg + Alt + Sfür Einstellungen öffnen- Editor → Code Style → Python
- „Use tab character“ deaktivieren
- Tabs auf 4 Spaces einstellen
Beispielcode: Prüfung bestanden?
note = 14
if note >= 10:
print(„Herzlichen Glückwunsch! Du hast bestanden.“)
else:
print(„Leider nicht bestanden.“)
Herzlichen Glückwunsch! Du hast bestanden.
Innerhalb einer Klasse:
note = 14
if note >= 10:
print(„Herzlichen Glückwunsch! Du hast bestanden.“)
else:
print(„Leider nicht bestanden.“)
Herzlichen Glückwunsch! Du hast bestanden.
Lektion 4: Variablentypen in Python (Detaillierte Erklärung)
Inhaltsübersicht:
Was sind Variablen?
Variablen sind benannte Speicherplätze im Arbeitsspeicher, die während der Programmausführung Daten aufnehmen. Sie ermöglichen es, Werte zu speichern, zu verändern und wiederzuverwenden.
Wichtig: Variablen helfen, Programme flexibel und nachvollziehbar zu gestalten. Sie können verschiedene Datentypen aufnehmen und sind ein zentrales Element jeder Programmiersprache.
print(projekt_nummer)
1201
Hinweis: In Python muss bei der Erstellung einer Variable sofort ein Wert zugewiesen werden. Der Name sollte beschreibend sein und keine Leerzeichen oder Sonderzeichen enthalten.
Mehrere Variablen mit dem gleichen Wert definieren
Manchmal möchte man mehrere Variablen auf denselben Wert setzen. In Python geht das in einer Zeile. Alle Variablen zeigen dann auf denselben Wert im Speicher.
print(firma, abteilung, standort)
TechNova TechNova TechNova
Technischer Hinweis: Alle Variablen referenzieren denselben Wert im Speicher. Ändert man den Wert einer Variable, sind die anderen nicht betroffen, wenn es sich um unveränderliche Datentypen wie str handelt.
Typ einer Variable herausfinden
Python erkennt den Typ einer Variable automatisch anhand des zugewiesenen Wertes. Mit type() kann man den Typ abfragen.
Warum ist das wichtig? Der Typ bestimmt, welche Operationen mit der Variable möglich sind.
print(type(budget)) # <class ‚int‘>
kommentar = „Projektfreigabe“
print(type(kommentar)) # <class ’str‘>
Dynamische Typisierung: In Python kann sich der Typ einer Variable im Programmverlauf ändern. Das macht Python flexibel, aber man muss aufpassen, dass die Typen zu den Operationen passen.
Grundlegende Variablentypen in Python
| Typ | Beschreibung | Beispiel |
|---|---|---|
| int | Ganze Zahlen, z. B. für Zählungen oder IDs | anzahl = 100 |
| float | Kommazahlen, z. B. für Messwerte oder Preise | gewicht = 72.5 |
| complex | Komplexe Zahlen mit Imaginärteil, selten im Alltag | impedanz = 3 + 4j |
b = 9.81
c = 2 + 5j
print(type(a))
print(type(b))
print(type(c))
Details:
int ist für ganze Zahlen ohne Komma.
float ist für Zahlen mit Dezimalstellen.
complex ist für mathematische Berechnungen mit Imaginärteil.
Texte (str)
Zeichenketten (str) sind für Text. Sie können mit einfachen (' ') oder doppelten (" ") Anführungszeichen geschrieben werden.
Mehrzeilige Strings werden mit drei Anführungszeichen (''' ''' oder """ """) erstellt.
mehrzeilig = “’Tag 1: Grundlagen
Tag 2: Vertiefung
Tag 3: Abschluss“‘
print(einzeilig)
print(mehrzeilig)
String-Methoden: Strings besitzen viele Methoden, z. B. .upper(), .lower(), .replace(), .split().
Boolesche Werte (bool)
Boolesche Werte (True oder False) sind wichtig für Bedingungen und Steuerung des Programmablaufs.
Sie entstehen oft durch Vergleiche (==, >, <).
if zugelassen:
print(„Teilnahme erlaubt“)
else:
print(„Zugang verweigert“)
Zugang verweigert
Praxis: Boolesche Werte werden oft in if-Abfragen genutzt, um Entscheidungen im Programm zu treffen.
Datenstrukturen in Python
Datenstrukturen sind spezielle Variablentypen, die mehrere Werte speichern können. Sie sind essenziell für die Organisation und Verarbeitung von Daten.
🔹 list – Veränderbare Reihenfolge
- Reihenfolge: Ja
- Veränderbar: Ja
- Duplikate: Erlaubt
produkte.append(„Monitor“)
print(produkte)
print(„Anzahl:“, len(produkte))
Details: Listen sind sehr flexibel. Man kann Elemente hinzufügen, entfernen und sortieren. Sie werden mit [] geschrieben.
🔹 tuple – Unveränderliche Liste
- Reihenfolge: Ja
- Veränderbar: Nein
- Duplikate: Erlaubt
print(quartale)
print(„Zweites Quartal:“, quartale[1])
Details: Tupel sind wie Listen, aber unveränderlich. Sie werden mit () geschrieben.
🔹 set – Ungeordnete Sammlung
- Reihenfolge: Nein
- Veränderbar: Ja
- Duplikate: Nicht erlaubt
print(tags)
print(„Anzahl:“, len(tags))
Details: Sets sind Mengen ohne Reihenfolge und ohne Duplikate. Sie werden mit {} geschrieben.
🔹 dict – Schlüssel-Wert-Paare
- Reihenfolge: Ja (ab Python 3.7)
- Veränderbar: Ja
- Duplikate bei Keys: Nicht erlaubt
„Name“: „Sven“,
„Position“: „Data Analyst“,
„Vollzeit“: True
}
print(„Name:“, mitarbeiter[„Name“])
Details: Dictionaries speichern Werte unter einem Schlüssel. Sie sind sehr praktisch für strukturierte Daten.
Alles ist ein Objekt
In Python ist alles ein Objekt. Das bedeutet, jede Variable besitzt Methoden und Attribute, die man nutzen kann.
Beispiel: Strings haben Methoden wie .upper(), .lower(), .replace().
print(sprache.upper()) # Methode upper() macht alles groß
PYTHON
Details: Auch Zahlen, Listen und Dictionaries sind Objekte und besitzen Methoden.
Fazit
Variablen sind die Grundlage jeder Programmierlogik. Python bietet mit seinen dynamischen Datentypen eine flexible Handhabung.
Ob Zahlen, Texte oder komplexe Datenstrukturen: Das Verständnis der Variablentypen ist essenziell für das effiziente Programmieren in Python.
Tipp: Experimentiere mit verschiedenen Typen und Methoden, um Python besser zu verstehen!
Lektion 5: Operatoren in Python
Das Konzept der Operatoren
Operatoren sind Symbole oder Schlüsselwörter, mit denen du Werte und Variablen in Python verarbeiten kannst. Sie ermöglichen mathematische Berechnungen, Vergleiche, logische Verknüpfungen und vieles mehr. Das Verständnis der Operatoren ist essenziell für jede Programmieraufgabe.
Arithmetische Operatoren
Arithmetische Operatoren führen mathematische Operationen aus. Sie sind die Grundlage für Berechnungen in Python.
| Bezeichnung | Symbol | Beispiel | Beschreibung | Demo |
|---|---|---|---|---|
| Zuweisung | = | a = b | Weist der Variable a den Wert von b zu. | |
| ||||
| Addition | + | a + b | Addiert die Werte von a und b. | |
| ||||
| Subtraktion | – | a – b | Subtrahiert b von a. | |
| ||||
| Multiplikation | * | a * b | Multipliziert a mit b. | |
| ||||
| Division | / | a / b | Teilt a durch b (Ergebnis ist eine Fließkommazahl). | |
| ||||
| Ganzzahlige Division | // | a // b | Teilt a durch b und gibt den ganzzahligen Anteil zurück. | |
| ||||
| Modulo | % | a % b | Gibt den Rest der Division von a durch b zurück. | |
| ||||
| Potenzierung | ** | a ** b | Erhöht a auf die Potenz b. | |
| ||||
Vergleichsoperatoren
Vergleichsoperatoren vergleichen zwei Werte und liefern True oder False.
| Bezeichnung | Symbol | Beispiel | Beschreibung | Demo |
|---|---|---|---|---|
| Gleich | == | a == b | Gibt True zurück, wenn a gleich b ist. | |
| ||||
| Ungleich | != | a != b | Gibt True zurück, wenn a ungleich b ist. | |
| ||||
| Größer als | > | a > b | Gibt True zurück, wenn a größer als b ist. | |
| ||||
| Kleiner als | < | a < b | Gibt True zurück, wenn a kleiner als b ist. | |
| ||||
| Größer oder gleich | >= | a >= b | Gibt True zurück, wenn a größer oder gleich b ist. | |
| ||||
| Kleiner oder gleich | <= | a <= b | Gibt True zurück, wenn a kleiner oder gleich b ist. | |
| ||||
Bitweise Operatoren
Bitweise Operatoren arbeiten auf der Binärdarstellung von Ganzzahlen. Sie sind nützlich für Systemprogrammierung und Hardwaresteuerung.
| Name | Symbol | Beispiel | Erklärung | Demo |
|---|---|---|---|---|
| Bitweises UND | & | a & b | Gibt nur die Bits zurück, die in beiden Operanden 1 sind. | |
| ||||
| Bitweises ODER | | | a | b | Gibt Bits zurück, die in mindestens einem der Operanden 1 sind. | |
| ||||
| Bitweises exklusives ODER | ^ | a ^ b | Gibt Bits zurück, die nicht gleichzeitig 1 in beiden Operanden sind. | |
| ||||
| Bitweise Negation | ~ | ~a | Invertiert alle Bits. Entspricht -a - 1. | |
| ||||
| Linksverschiebung | << | a << 2 | Verschiebt die Bits um 2 Stellen nach links. Entspricht a * 4. | |
| ||||
| Rechtsverschiebung | >> | a >> 2 | Verschiebt die Bits um 2 Stellen nach rechts. Entspricht a // 4. | |
| ||||
Identitätsoperatoren
Identitätsoperatoren prüfen, ob zwei Variablen auf dasselbe Objekt im Speicher zeigen. Sie sind besonders wichtig beim Vergleich von Listen, Dictionaries und anderen komplexen Datentypen.
| Name | Symbol | Beispiel | Erklärung | Demo |
|---|---|---|---|---|
| is | is | a is b | Gibt True zurück, wenn a und b dasselbe Objekt sind (gleiche Speicheradresse). | |
| ||||
| is not | is not | a is not b | Gibt True zurück, wenn a und b nicht dasselbe Objekt sind. | |
| ||||
| is (Zahlen) | is | x is y | Vergleich mit Zahlen (Achtung: kleine Zahlen können intern gleich sein!) | |
| ||||
Tipp: is prüft die Identität (Speicheradresse), == prüft den Wert. Zwei Listen mit gleichem Inhalt sind == gleich, aber nur is gleich, wenn sie dasselbe Objekt sind.
Lektion 6: Bedingungen & Verschachtelung in Python
Inhaltsübersicht:
Grundlagen von Bedingungen
Bedingungen (conditions) steuern den Ablauf eines Programms abhängig von bestimmten Kriterien. Mit ihnen kannst du verschiedene Aktionen ausführen, je nachdem, ob eine Bedingung erfüllt ist oder nicht.
Beispiel: Ist ein Nutzer angemeldet, darf er Daten bearbeiten. Ist er nicht angemeldet, bekommt er eine entsprechende Meldung.
Bedingungen können beliebig verschachtelt werden – also Bedingungen innerhalb von Bedingungen.
Haupt-Bedingungssätze
| Bezeichnung | Anwendungszweck |
|---|---|
| if | „wenn“ – führt Code aus, wenn die Bedingung erfüllt ist. |
| elif | „sonst wenn“ – prüft weitere Bedingungen, falls vorherige nicht zutrafen. |
| else | „ansonsten“ – wird ausgeführt, wenn keine vorherige Bedingung erfüllt wurde. |
Beispiele für Bedingungssätze
alter = 21
if alter >= 18:
print("Zugang erlaubt.")
Prüft, ob alter mindestens 18 ist. Wenn ja, wird die Meldung ausgegeben.
angemeldet = False
if angemeldet:
print("Fortschritt speichern möglich.")
else:
print("Bitte melden Sie sich an, um fortzufahren.")
Wenn angemeldet True ist, wird der erste Block ausgeführt, sonst der else-Block.
rolle = "redakteur"
if rolle == "administrator":
print("Zugriff für Administrator.")
elif rolle == "redakteur":
print("Zugriff für Redakteur.")
elif rolle == "autor":
print("Zugriff für Autor.")
else:
print("Zugriff für Gast.")
Es wird der erste zutreffende Block ausgeführt, danach werden die restlichen elif oder else-Blöcke übersprungen.
Logische Operatoren & verschachtelte Bedingungen
nummer = 15
if nummer >= 0 and nummer <= 20:
print("Nummer liegt im erlaubten Bereich.")
else:
print("Nummer nicht erlaubt.")
Beide Bedingungen müssen erfüllt sein (nummer zwischen 0 und 20).
wert = 3
if wert == 1 or wert == 2 or wert == 3:
print("Wert ist zulässig.")
else:
print("Wert ist nicht zulässig.")
Es reicht aus, wenn eine der Bedingungen erfüllt ist.
geschlecht = "weiblich"
alter = 17
if geschlecht == "männlich":
print("Geschlecht: männlich")
if alter < 21:
print("Er ist ein junger Mann.")
elif geschlecht == "weiblich":
print("Geschlecht: weiblich")
if alter < 21:
print("Sie ist ein junges Mädchen.")
Hier befindet sich eine Bedingung innerhalb einer anderen.
Verschachtelte Bedingungen – Praxis
mitgliederstatus = 'premium'
alter = 30
if mitgliederstatus == 'standard':
print('Standard-Mitgliedschaft erkannt.')
if alter < 18:
print('Eingeschränkter Zugang für Minderjährige.')
else:
print('Voller Zugang für erwachsene Standard-Mitglieder.')
elif mitgliederstatus == 'premium':
print('Premium-Mitgliedschaft erkannt.')
if alter < 18:
print('Jugendlicher Premium-Zugang mit zusätzlichen Inhalten.')
else:
print('Voller Premium-Zugang mit exklusiven Vorteilen.')
else:
print('Mitgliedschaft unbekannt – bitte anmelden.')
Premium-Mitgliedschaft erkannt.
Voller Premium-Zugang mit exklusiven Vorteilen.
- Der Interpreter prüft zuerst, ob
mitgliederstatus'standard'ist. - Da
mitgliederstatus'premium'ist, wird diese Bedingung übersprungen. - Python prüft
elif:mitgliederstatus == 'premium'– das trifft zu, also wird dieser Block ausgeführt. - Innerhalb dieses Blocks wird
alter < 18geprüft. Daalter30 ist, wird dieelse-Anweisung ausgeführt.
Zusammenfassung
Verschachtelte Bedingungen sind ein fundamentaler Bestandteil der Programmierung. Sie erlauben es, komplexe Entscheidungsbäume abzubilden und verschiedene Eingabekombinationen differenziert zu behandeln.
In Python werden solche Bedingungen mit Einrückungen dargestellt, wodurch der Code übersichtlich und gut lesbar bleibt.
Nutze if, elif und else sowie logische Operatoren, um flexible und präzise Programmabläufe zu gestalten.
Lektion 7: Schleifen in Python – Ein umfassender Überblick
Inhaltsübersicht:
Einführung in das Konzept von Schleifen
Schleifen sind ein zentrales Konzept in der Programmierung und ermöglichen die wiederholte Ausführung von Codeblöcken. In Python dienen Schleifen dazu, bestimmte Anweisungen mehrfach auszuführen – entweder eine fest definierte Anzahl von Durchläufen oder so lange, wie eine Bedingung erfüllt ist. Dies reduziert Redundanz, erhöht die Effizienz und macht Programme flexibler.
Schleifentypen in Python
| Schleifentyp | Beschreibung |
|---|---|
| for-Schleife | Wird verwendet, um über Sequenzen wie Listen, Zeichenketten oder Bereiche (range) zu iterieren. Sie eignet sich besonders für bekannte Durchlaufmengen. |
| while-Schleife | Führt den Code aus, solange eine bestimmte Bedingung True ergibt. Sie eignet sich, wenn die Anzahl der Wiederholungen nicht im Voraus bekannt ist. |
1. Die for-Schleife
Die for-Schleife in Python erlaubt es, über jedes Element einer Sequenz zu iterieren – sei es eine Liste, ein String oder ein durch range() erzeugter Bereich. Dabei entfällt die manuelle Definition eines Zählers, wie es in vielen anderen Sprachen notwendig ist.
for element in sequence:
# Anweisungen
element: Eine temporäre Variable, die in jedem Schleifendurchlauf ein neues Element der Sequenz annimmt.
sequence: Eine iterierbare Datenstruktur (z. B. Liste, Tuple, String).
Die eingerückten Anweisungen werden in jedem Schleifendurchlauf ausgeführt.
Beispiel 1: Iteration über eine Liste
wochentage = ['Montag', 'Dienstag', 'Mittwoch', 'Donnerstag', 'Freitag']
for tag in wochentage:
print(f"Heute ist {tag}")
Heute ist Dienstag
Heute ist Mittwoch
Heute ist Donnerstag
Heute ist Freitag
Beispiel 2: Iteration über Zeichen in einem String
text = "Python"
for buchstabe in text:
print(f"Buchstabe: {buchstabe}")
Buchstabe: y
Buchstabe: t
Buchstabe: h
Buchstabe: o
Buchstabe: n
Die Funktion range()
Die Funktion range() erzeugt eine Folge von Ganzzahlen und wird häufig in Kombination mit der for-Schleife verwendet.
for i in range(1, 6):
print(i)
2
3
4
5
Absteigende Iteration:
for i in range(5, 0, -1):
print(i)
4
3
2
1
2. Die while-Schleife
Die while-Schleife führt eine Anweisung so lange aus, wie eine Bedingung erfüllt ist (True). Sie ist ideal für Situationen, in denen nicht im Voraus feststeht, wie oft ein Vorgang wiederholt werden soll.
zähler = 1
while zähler <= 5:
print(zähler)
zähler += 1
2
3
4
5
else-Block mit while
x = 1
while x <= 3:
print(x)
x += 1
else:
print("Bedingung nicht mehr erfüllt.")
2
3
Bedingung nicht mehr erfüllt.
Unendliche Schleifen (Infinite Loops)
while True:
print("Ich höre nie auf!")
⚠ Achtung: Unendliche Schleifen können Programme blockieren und das System belasten.
Kontrollanweisungen in Schleifen
Kontrollanweisungen ermöglichen eine flexible Steuerung des Ablaufs innerhalb von Schleifen. Zu den wichtigsten gehören:
- break: Beendet die Schleife vollständig, sobald sie erreicht wird.
- continue: Springt zur nächsten Iteration und überspringt den restlichen Code der aktuellen Schleifendurchlaufes.
Beispiel: break
for zahl in range(1, 10):
if zahl == 5:
break
print(zahl)
2
3
4
Beispiel: continue (Nur ungerade Zahlen ausgeben)
for zahl in range(1, 7):
if zahl % 2 == 0:
continue
print(zahl)
3
5
Gültigkeitsbereich von Variablen in Schleifen
In Python bleiben Variablen, die innerhalb einer Schleife deklariert wurden, auch außerhalb der Schleife gültig. Das unterscheidet Python von vielen anderen Sprachen.
for i in range(3):
print(i)
print("Letzter Wert von i:", i)
1
2
Letzter Wert von i: 2
Fazit
Python bietet eine intuitive und flexible Handhabung von Schleifen. Die for-Schleife eignet sich hervorragend für Iterationen über Sequenzen, während die while-Schleife für bedingungsbasierte Wiederholungen ideal ist. Kontrollanweisungen wie break und continue erweitern die Steuerungsmöglichkeiten erheblich. Das Verständnis dieser Konzepte ist essenziell für saubere, effiziente und lesbare Python-Programme.
Lektion 8: Arbeiten mit Zahlen
Inhaltsübersicht:
Einleitung
Diese Lerneinheit vermittelt ein fundiertes Verständnis über die in Python verfügbaren Zahlentypen. Neben der Differenzierung zwischen ganzzahligen, gleitkomma- sowie komplexen Zahlen widmen wir uns ebenfalls den integrierten Funktionen der Sprache, die zur Typumwandlung, zur Durchführung arithmetischer Berechnungen und zur Generierung von Zufallswerten eingesetzt werden können.
Ein wesentliches Merkmal numerischer Datentypen in Python ist ihre Unveränderlichkeit (Immutability). Das bedeutet: Wird einer Variablen ein numerischer Wert zugewiesen, reserviert das System einen bestimmten Speicherbereich. Sobald dieser Variablen jedoch ein neuer Wert zugewiesen wird, erfolgt keine direkte Überschreibung, sondern eine Neuzuweisung in einem separaten Speicherbereich. Der zuvor belegte Speicher wird anschließend – in der Regel automatisch – vom sogenannten Garbage Collector freigegeben, welcher in Python für das effiziente Speicher- und Ressourcenmanagement zuständig ist.
Zahlentypen in Python
| Datentyp | Beschreibung | Beispiel |
|---|---|---|
| int | Repräsentiert ganze Zahlen ohne Nachkommastellen | wert_1 = 10 |
| float | Stellt Gleitkommazahlen (Zahlen mit Dezimalpunkt) dar | wert_2 = 3.14 |
| complex | Modelliert komplexe Zahlen mit realem und imaginärem Anteil | wert_3 = 2 + 5j |
j angegeben, welcher für √-1 steht – eine Konvention, die insbesondere in technischen und naturwissenschaftlichen Kontexten Anwendung findet.wert_1 = 10 # Ganze Zahl (Integer)
wert_2 = 3.14 # Dezimalzahl (Float)
wert_3 = complex(2, 5) # Komplexe Zahl mit Realteil = 2 und Imaginärteil = 5
# Typausgabe
print(„Typ von wert_1:“, type(wert_1))
print(„Typ von wert_2:“, type(wert_2))
print(„Typ von wert_3:“, type(wert_3))
Typ von wert_2: <class ‚float‘>
Typ von wert_3: <class ‚complex‘>
Durch diese automatische Typisierung wird die Handhabung numerischer Werte in Python deutlich vereinfacht und fördert eine intuitive, leserfreundliche Programmierung.
Darstellung von Ganzzahlen in verschiedenen Zahlensystemen
Python erlaubt es, ganze Zahlen nicht nur im bekannten Dezimalsystem (Basis 10), sondern auch im Binärsystem (Basis 2), Oktalsystem (Basis 8) und Hexadezimalsystem (Basis 16) darzustellen. Diese Flexibilität ist besonders im Bereich der Softwareentwicklung mit Hardwarebezug, bei Netzwerkanwendungen oder auch in der Kryptographie hilfreich.
| Zahlensystem | Präfix | Beispiel | Entsprechender Dezimalwert |
|---|---|---|---|
| Binär | 0b | 0b1010 | 10 |
| Oktal | 0o | 0o17 | 15 |
| Dezimal | (keiner) | 25 | 25 |
| Hexadezimal | 0x | 0x1F | 31 |
dezimalzahl = 42 # Normale Dezimalzahl
binaerzahl = 0b101010 # Binärdarstellung von 42
oktalzahl = 0o52 # Oktaldarstellung von 42
hexzahl = 0x2A # Hexadezimaldarstellung von 42
# Ausgaben der Werte
print(„Dezimal:“, dezimalzahl)
print(„Binär (0b101010):“, binaerzahl)
print(„Oktal (0o52):“, oktalzahl)
print(„Hexadezimal (0x2A):“, hexzahl)
# Typprüfung
print(„Typ von hexzahl:“, type(hexzahl))
Binär (0b101010): 42
Oktal (0o52): 42
Hexadezimal (0x2A): 42
Typ von hexzahl: <class ‚int‘>
int) im Dezimalformat. Die verschiedenen Notationen dienen lediglich der besseren Lesbarkeit und Anwendbarkeit in bestimmten Kontexten.Typumwandlung numerischer Werte in Python
Python bietet eine Reihe integrierter Funktionen zur expliziten Typkonvertierung, mit denen sich Zahlen zwischen verschiedenen Datentypen konvertieren lassen. Solche Konvertierungen sind insbesondere dann relevant, wenn etwa Benutzereingaben als Zeichenkette (String) vorliegen oder wenn Berechnungen mit unterschiedlichen Zahlentypen harmonisiert werden sollen.
int(x) – Umwandlung in einen Ganzzahltyp
- Funktionssignatur:
int(x=0) - Parameter: x – Ein Wert beliebigen Typs, der numerisch interpretierbar sein muss (z. B. Float, String mit Ziffern etc.).
- Gültige Eingaben:
int("42")→ erlaubtint(3.9)→ erlaubtint(" 42 ")→ nicht erlaubt, da Leerzeichen enthalten sind
• Wird ein Dezimalwert (float) übergeben, wird die Nachkommastelle abgeschnitten, nicht gerundet.
• Bei Zeichenketten darf die Zeichenfolge ausschließlich aus Ziffern bestehen, andernfalls wird ein Fehler ausgelöst.
wert_float = 5.9
wert_int = int(wert_float)
print(„Ursprünglicher Wert:“, wert_float)
print(„Nach Umwandlung mit int():“, wert_int)
Nach Umwandlung mit int(): 5
text = „123“
zahl = int(text)
print(„Eingegebener Text:“, text)
print(„Konvertierter Wert:“, zahl)
Konvertierter Wert: 123
int() ist tolerant gegenüber numerischen Werten mit anderen Typen, jedoch strikt bei der Verarbeitung von Strings – kein Text, keine Sonderzeichen oder Leerzeichen dürfen enthalten sein.int(x, base) – Umwandlung von Zeichenketten in Ganzzahlen mit Basisangabe
- Funktionssignatur:
int(x, base=10) - Parameter:
- x: Eine Zeichenkette, die eine ganze Zahl in der entsprechenden Basis repräsentiert, z. B.
"1010"für Binär oder"1F"für Hexadezimal. - base: Ein ganzzahliger Wert zwischen 2 und 36, der die numerische Basis (das Zahlensystem) angibt. Standardwert ist 10 (Dezimalsystem).
- x: Eine Zeichenkette, die eine ganze Zahl in der entsprechenden Basis repräsentiert, z. B.
Die Funktion interpretiert die Zeichenkette
x gemäß der angegebenen Basis und gibt den entsprechenden Dezimalwert als int zurück.| Basis | Bedeutung | Beispiel (x) | Ergebnis von int(x, base) |
|---|---|---|---|
| 2 | Binär | „101“ | 5 |
| 8 | Oktal | „17“ | 15 |
| 16 | Hexadezimal | „1F“ | 31 |
| 10 | Dezimal (Standard) | „42“ | 42 |
bin_str = „1010“ # Binäre Zeichenkette (entspricht 10 dezimal)
dezimal = int(bin_str, 2) # Basis 2 angeben
print(„Binär:“, bin_str)
print(„Dezimal:“, dezimal)
Dezimal: 10
hex_str = „A3“ # Hexadezimalwert (entspricht 163 dezimal)
dezimal = int(hex_str, 16) # Basis 16
print(„Hexadezimal:“, hex_str)
print(„Dezimal:“, dezimal)
Dezimal: 163
oktal_str = „52“ # Oktalwert (entspricht 42 dezimal)
dezimal = int(oktal_str, 8) # Basis 8
print(„Oktal:“, oktal_str)
print(„Dezimal:“, dezimal)
Dezimal: 42
int("19", 8) aufgerufen wird, da „9“ im Oktalsystem nicht existiert.float(x) – Umwandlung in eine Gleitkommazahl
- Funktionssignatur:
float(x) - Parameter: x: Ein numerischer Ausdruck (z. B. int, str oder sogar float). Auch Zeichenketten, die eine gültige Dezimalzahl enthalten, sind zulässig.
• Ganze Zahlen werden zu Fließkommazahlen umgewandelt (z. B. 5 → 5.0)
• Zeichenketten, die eine Dezimalzahl korrekt repräsentieren, werden in den entsprechenden float-Wert konvertiert
• Bei ungültigen Eingaben (z. B. nicht-numerische Strings) wird ein Fehler ausgelöst
ganzzahl = 7
dezimal = float(ganzzahl)
print(„Vorher (int):“, ganzzahl)
print(„Nachher (float):“, dezimal)
Nachher (float): 7.0
text = „3.1415“
wert = float(text)
print(„Eingegebener Text:“, text)
print(„Konvertierter Wert:“, wert)
Konvertierter Wert: 3.1415
ungültiger_text = „abc123“
wert = float(ungültiger_text) # Wird einen Fehler auslösen
• Die Funktion
float() ist tolerant gegenüber numerischen Eingaben, jedoch streng bei der Interpretation von Zeichenketten. Der Inhalt muss exakt einer gültigen Zahl entsprechen – keine zusätzlichen Zeichen oder Leerzeichen.• Auch negative Zahlen und wissenschaftliche Notation (z. B.
"1.2e3" → 1200.0) werden korrekt erkannt und konvertiert.complex(real, imag) – Erzeugung einer komplexen Zahl
- Funktionssignatur:
complex(real=0, imag=0) - Parameter:
- real: Der reale Anteil der Zahl. Kann vom Typ int, float oder eine Zeichenkette mit numerischem Inhalt sein.
- imag: Der imaginäre Anteil der Zahl (optional). Auch hier sind int, float oder numerische Strings erlaubt.
• Gibt eine komplexe Zahl der Form a + bj zurück, wobei:
• a der Realteil ist,
• b der Imaginärteil (mit j als Imaginäreinheit).
• Wird nur ein Argument übergeben, wird der Imaginärteil standardmäßig auf 0 gesetzt.
• Die Darstellung erfolgt in Python stets mit einem kleinen „j“: z. B. 3 + 2j.
z = complex(3, 4)
print(„Komplexe Zahl:“, z)
print(„Typ:“, type(z))
Typ: <class ‚complex‘>
z = complex(5)
print(„Komplexe Zahl (nur Realteil):“, z)
z = complex(„2.5“, „1.5“)
print(„Komplexe Zahl (aus Strings):“, z)
• Python verwendet die mathematische Schreibweise mit „j“ zur Darstellung imaginärer Zahlen – analog zu √-1.
• Für komplexe Zahlen existieren zusätzliche Funktionen und Eigenschaften, z. B.:
•
z.real → gibt den Realteil zurück•
z.imag → gibt den Imaginärteil zurück•
abs(z) → Betrag der komplexen Zahl (Wurzel aus a² + b²)Funktionen zur Arbeit mit Zahlen
In Python ist die Flexibilität beim Umgang mit verschiedenen Zahlentypen ein zentraler Bestandteil der Sprache. Um sicherzustellen, dass numerische Werte korrekt verarbeitet, verglichen oder weiterverwendet werden können, stellt Python mehrere eingebaute Funktionen bereit.
Diese Funktionen ermöglichen es, Werte gezielt in andere numerische Typen umzuwandeln – z. B. von Gleitkomma- zu Ganzzahlen, von Text zu Zahlen oder zur Bildung komplexer Zahlen. Dies ist besonders wichtig bei der Verarbeitung von Benutzereingaben, bei mathematischen Operationen mit gemischten Datentypen sowie in wissenschaftlichen Berechnungen.
abs(x) – Betrag (Absolutwert) einer Zahl
Die Funktion abs() dient zur Berechnung des Absolutwerts einer Zahl – d. h. sie gibt stets den positiven Wert einer gegebenen Zahl zurück, unabhängig davon, ob der ursprüngliche Wert negativ war oder nicht.
Diese Funktion ist in Python integriert (built-in) und kann mit allen numerischen Typen verwendet werden: int, float sowie auch mit complex.
- Funktionssignatur:
abs(x) - Parameter: x: Eine Zahl vom Typ int, float oder complex.
• Bei ganzen Zahlen (int) und Gleitkommazahlen (float) gibt abs() den positiven Wert zurück.
• Bei komplexen Zahlen wird der Betrag (Modul) der Zahl berechnet:
|a + bj| = √(a² + b²)
x = -12
ergebnis = abs(x)
print(„Betrag von“, x, „ist:“, ergebnis)
x = -7.5
print(„Betrag von“, x, „ist:“, abs(x))
z = complex(3, 4) # entspricht 3 + 4j
betrag = abs(z) # √(3² + 4²) = 5.0
print(„Betrag von“, z, „ist:“, betrag)
abs() ist besonders nützlich in der numerischen Mathematik, etwa bei Differenzberechnungen, Abstandsmessungen, Fehleranalysen oder im Bereich der komplexen Zahlenrechnung.round(x[, n]) – Rundung einer Zahl
Die Funktion round() rundet eine Zahl auf eine definierte Anzahl von Nachkommastellen. Standardmäßig wird auf die nächste ganze Zahl gerundet, wenn die Anzahl der Nachkommastellen nicht angegeben wird.
- Funktionssignatur:
round(x[, n]) - Parameter:
- x: Eine Zahl vom Typ int oder float, die gerundet werden soll.
- n (optional): Anzahl der Dezimalstellen, auf die gerundet werden soll (int). Standardwert ist 0.
• Ohne Angabe von n wird x auf die nächstliegende ganze Zahl gerundet.
• Mit Angabe von n wird x auf n Nachkommastellen gerundet.
• Bei Halbwerten (.5) rundet Python nach der „Banker’s rounding“-Regel (auf die nächste gerade Zahl).
x = 7.6
ergebnis = round(x)
print(„Gerundet:“, ergebnis)
x = 3.14159
print(„Gerundet auf 2 Stellen:“, round(x, 2))
print(round(2.5)) # Ausgabe: 2
print(round(3.5)) # Ausgabe: 4
4
round() wird häufig in der Finanzmathematik, bei der Anzeige von Ergebnissen mit begrenzter Nachkommastellenanzahl oder bei Näherungsberechnungen verwendet.max(x1, x2, …) – Maximum aus mehreren Werten
Die Funktion max() gibt das größte Element aus einer Reihe von Werten oder aus einer iterierbaren Datenstruktur zurück.
- Funktionssignatur:
max(iterable, *[, key, default])odermax(arg1, arg2, *args, *[, key]) - Parameter:
- arg1, arg2, *args: Zwei oder mehr Werte, aus denen das Maximum ermittelt wird.
- iterable: Eine iterierbare Datenstruktur (z. B. Liste, Tuple, Set).
- key (optional): Eine Funktion, die auf jedes Element angewendet wird, um den Vergleichswert zu bestimmen.
- default (optional): Wert, der zurückgegeben wird, wenn das Iterable leer ist (nur bei Iterable-Variante).
• Ohne key wird der natürliche Größenvergleich verwendet.
• Gibt den größten Wert zurück.
• Wenn mehrere Werte gleich groß sind, wird der erste davon zurückgegeben.
• Bei leerem Iterable und ohne default wird eine ValueError ausgelöst.
ergebnis = max(5, 10, 3, 8)
print(„Maximalwert:“, ergebnis)
zahlen = [4, 15, 2, 9]
print(„Maximalwert aus Liste:“, max(zahlen))
worte = [„Apfel“, „Birne“, „Banane“]
# Länge der Wörter als Vergleichskriterium
langstes_wort = max(worte, key=len)
print(„Längstes Wort:“, langstes_wort)
max() ist nützlich, um aus Datensätzen den höchsten Wert zu ermitteln, sei es bei Zahlen, Strings oder komplexeren Datenstrukturen durch Verwendung des key-Parameters.min(x1, x2, …) – Minimum aus mehreren Werten
Die Funktion min() gibt das kleinste Element aus einer Reihe von Werten oder aus einer iterierbaren Datenstruktur zurück.
- Funktionssignatur:
min(iterable, *[, key, default])odermin(arg1, arg2, *args, *[, key]) - Parameter:
- arg1, arg2, *args: Zwei oder mehr Werte, aus denen das Minimum ermittelt wird.
- iterable: Eine iterierbare Datenstruktur (z. B. Liste, Tuple, Set).
- key (optional): Eine Funktion, die auf jedes Element angewendet wird, um den Vergleichswert zu bestimmen.
- default (optional): Wert, der zurückgegeben wird, wenn das Iterable leer ist (nur bei Iterable-Variante).
• Ohne key wird der natürliche Größenvergleich verwendet.
• Gibt den kleinsten Wert zurück.
• Wenn mehrere Werte gleich klein sind, wird der erste davon zurückgegeben.
• Bei leerem Iterable und ohne default wird eine ValueError ausgelöst.
ergebnis = min(5, 10, 3, 8)
print(„Minimalwert:“, ergebnis)
zahlen = [4, 15, 2, 9]
print(„Minimalwert aus Liste:“, min(zahlen))
worte = [„Apfel“, „Birne“, „Banane“]
# Länge der Wörter als Vergleichskriterium
kürzestes_wort = min(worte, key=len)
print(„Kürzestes Wort:“, kürzestes_wort)
min() wird verwendet, um aus Datensätzen den kleinsten Wert zu ermitteln, sei es bei Zahlen, Strings oder komplexeren Datenstrukturen durch Verwendung des key-Parameters.Bedeutung des Begriffs Modul
Ein Modul in Python ist eine eigenständige Datei, die Funktionen, Klassen, Variablen und weitere Bestandteile enthalten kann.
Um die Inhalte eines Moduls im eigenen Programm verwenden zu können, wird es mit dem Schlüsselwort import eingebunden. Anschließend stehen alle definierten Bestandteile direkt zur Verfügung.
Im weiteren Verlauf dieser Lernreihe wirst du Schritt für Schritt lernen, wie man eigene Module erstellt und effektiv einsetzt.
Zudem wirst du eine Vielzahl an nützlichen, bereits integrierten Modulen aus der Python-Standardbibliothek kennenlernen.
In diesem Abschnitt werfen wir einen genaueren Blick auf zwei häufig verwendete Module: math für mathematische Berechnungen und random zur Erzeugung von Zufallswerten.
Variablen und Konstanten des Moduls math
Das Python-Modul math stellt neben zahlreichen mathematischen Funktionen auch wichtige Konstanten und spezielle Variablen zur Verfügung, die in vielen mathematischen und wissenschaftlichen Anwendungen benötigt werden.
Diese Konstanten sind direkt im Modul definiert und können nach dem Import sofort verwendet werden.
import math
| Name | Beschreibung | Beispielwert |
|---|---|---|
| math.pi | Die Kreiszahl π (Pi) – Verhältnis von Kreisumfang zu Durchmesser | 3.141592653589793 |
| math.e | Die Eulersche Zahl – Basis des natürlichen Logarithmus | 2.718281828459045 |
| math.tau | Der doppelte Wert von π – entspricht einem Vollkreis in Radiant | 6.283185307179586 |
| math.inf | Stellt eine positive Unendlichkeit dar | ∞ |
| -math.inf | Negative Unendlichkeit | -∞ |
| math.nan | „Not a Number“ – steht für undefinierte oder ungültige Rechenergebnisse | NaN |
import math
# Kreisumfang berechnen mit Radius r = 5
r = 5
umfang = 2 * math.pi * r
print(„Kreisumfang:“, umfang)
# Verwendung der Eulerschen Zahl
wachstum = math.e ** 2
print(„e hoch 2:“, wachstum)
# Umgang mit Unendlichkeit
print(„Ist unendlich größer als 1000000?“, math.inf > 1_000_000)
# NaN – Beispiel bei ungültiger Operation
wert = math.nan
print(„Ist wert ein gültiger Wert?“, math.isnan(wert)) # True
• Konstanten wie
math.inf oder math.nan sind besonders nützlich beim Behandeln von Grenzfällen oder bei fehlerhaften Berechnungen (z. B. durch 0 teilen).•
math.tau ist in bestimmten Bereichen (z. B. Kreisberechnungen oder Fourier-Analysen) nützlicher als math.pi.Wichtigste Funktionen des Moduls math
ceil(x) – Aufrunden zur nächsten ganzen Zahl
Die Funktion math.ceil(x) rundet eine gegebene Zahl immer auf die nächstgrößere ganze Zahl auf, unabhängig vom Nachkommabetrag. Sie ist besonders nützlich, wenn man sicherstellen möchte, dass das Ergebnis nicht kleiner als der ursprüngliche Wert ist – beispielsweise bei Mengenkalkulationen oder der Reservierung ganzer Einheiten.
- Funktionssignatur:
math.ceil(x) - Parameter: x: Eine Gleitkommazahl (float) oder ein ganzzahliger Wert (int)
- Rückgabewert: Gibt den kleinsten ganzzahligen Wert zurück, der größer oder gleich x ist. Der Rückgabewert hat den Datentyp int.
import math
wert = 4.2
ergebnis = math.ceil(wert)
print(„Ergebnis von ceil(4.2):“, ergebnis)
wert = -4.2
print(„Ergebnis von ceil(-4.2):“, math.ceil(wert))
• Reservierung fester Ressourcen (z. B. mindestens 3,4 GB → 4 GB)
• Rundung von Preisen oder Mengen nach oben
• Berechnungen mit Raten, bei denen man keine Teilmengen zulässt
floor(x) – Abrunden zur nächstkleineren ganzen Zahl
Die Funktion math.floor(x) rundet eine gegebene Zahl immer auf die nächstkleinere ganze Zahl ab, unabhängig davon, wie nahe sie an der nächsten Ganzzahl liegt. Sie ist das Gegenstück zu ceil(x).
- Funktionssignatur:
math.floor(x) - Parameter: x: Eine Gleitkommazahl (float) oder ein ganzzahliger Wert (int)
- Rückgabewert: Gibt den größten ganzzahligen Wert zurück, der kleiner oder gleich x ist. Der Rückgabewert ist vom Typ int.
import math
wert = 7.9
ergebnis = math.floor(wert)
print(„Ergebnis von floor(7.9):“, ergebnis)
wert = -3.1
print(„Ergebnis von floor(-3.1):“, math.floor(wert))
floor() weiter ins Negative, also weg von 0.• Kalkulation von Speicherplätzen, bei denen keine Teilwerte zulässig sind
• Positionierung und Indizierung, z. B. in Arrays oder Koordinatensystemen
• Mathematische Simulationen, bei denen abrundende Logik benötigt wird
pow(x, y) – Potenzieren (x hoch y)
Die Funktion math.pow(x, y) berechnet die Potenz von zwei Zahlen, d. h. sie hebt die Zahl x zur Potenz y:
math.pow(x, y) = xy
- Funktionssignatur:
math.pow(x, y) - Parameter:
- x: Die Basis (Zahl, die potenziert wird)
- y: Der Exponent (Zahl, auf die potenziert wird)
- Rückgabewert: Gibt das Ergebnis von
xyals Gleitkommazahl (float) zurück – auch wenn das Ergebnis eine ganze Zahl ist.
import math
ergebnis = math.pow(2, 3)
print(„2 hoch 3 ist:“, ergebnis)
print(„4 hoch -2 ist:“, math.pow(4, -2))
** (Potenzierungsoperator):In Python kann man auch mit dem Operator
** potenzieren:print(2 ** 3) # ergibt 8 (als int)Unterschied:
•
** gibt je nach Eingabe int oder float zurück•
math.pow() gibt immer einen float zurück und gehört zur mathematischen Standardbibliothek• Wissenschaftliche Berechnungen, z. B. in der Physik oder Statistik
• Exponentialfunktionen in Simulationen oder Finanzberechnungen
• Wachstumsmodelle und Skalierungen
sqrt(x) – Quadratwurzel berechnen
Die Funktion math.sqrt(x) berechnet die Quadratwurzel einer Zahl, also die Zahl, die mit sich selbst multipliziert das Argument x ergibt:
math.sqrt(x) = √x
- Funktionssignatur:
math.sqrt(x) - Parameter: x: Eine nicht-negative Zahl (int oder float), von der die Quadratwurzel berechnet werden soll.
- Rückgabewert: Gibt die Quadratwurzel von x als Gleitkommazahl (float) zurück.
import math
wert = 25
wurzel = math.sqrt(wert)
print(„Die Quadratwurzel von“, wert, „ist:“, wurzel)
print(„Quadratwurzel von 2:“, math.sqrt(2))
math.sqrt(-9) # ValueError: math domain error•
math.sqrt() akzeptiert keine negativen Zahlen, da es nur im Bereich der reellen Zahlen arbeitet.• Für komplexe Wurzeln kann stattdessen
cmath.sqrt() verwendet werden.• Geometrische Berechnungen, z. B. Abstandsberechnungen mit dem Satz des Pythagoras
• Statistik, z. B. bei der Berechnung der Standardabweichung
• Physik, z. B. für Geschwindigkeits- und Energieformeln
exp(x) – Exponentialfunktion berechnen
Die Funktion math.exp(x) berechnet den Exponentialwert der Zahl x, also:
math.exp(x) = ex
Dabei ist e die Eulersche Zahl (≈ 2.71828), eine wichtige mathematische Konstante, die u. a. in Naturwissenschaften, Statistik und Finanzmathematik eine zentrale Rolle spielt.
- Funktionssignatur:
math.exp(x) - Parameter: x: Eine reelle Zahl (int oder float), als Exponent der Eulerschen Zahl.
- Rückgabewert: Gibt den Wert von
exals Gleitkommazahl (float) zurück.
import math
wert = 2
ergebnis = math.exp(wert)
print(„e hoch“, wert, „ist:“, ergebnis)
print(„e hoch -1 ist:“, math.exp(-1))
• Wachstums- und Zerfallsprozesse, z. B. bei Zinsen, Bevölkerungswachstum oder radioaktivem Zerfall
• Berechnung von Wahrscheinlichkeiten, z. B. in der Normalverteilung (Gauß-Verteilung)
• Simulationen und Algorithmen, z. B. Softmax-Funktion im Machine Learning
exp() ist besonders dann nützlich, wenn man mathematische Modelle aufbaut, bei denen Wachstum oder Verfall exponentiell ablaufen.log(x[, base]) – Logarithmus berechnen
Die Funktion math.log(x[, base]) berechnet den Logarithmus einer Zahl x zur angegebenen Basis base. Wird keine Basis angegeben, verwendet die Funktion automatisch die natürliche Basis e (≈ 2.71828).
- Funktionssignatur:
math.log(x, base)oder einfachmath.log(x)(entspricht ln(x)) - Parameter:
- x: Eine positive Zahl (int oder float)
- base (optional): Die Basis des Logarithmus (z. B. 2, 10, e)
- Rückgabewert: Gibt den Logarithmus von x zur angegebenen Basis als Gleitkommazahl (float) zurück.
Bedeutung:
math.log(x, b) = logb(x) bzw. math.log(x) = ln(x)
import math
print(„ln(10) =“, math.log(10))
print(„log₁₀(1000) =“, math.log(1000, 10))
print(„log₂(8) =“, math.log(8, 2))
• x muss positiv sein – andernfalls tritt ein ValueError auf:
math.log(0) # ValueError: math domain errormath.log(-5) # ValueError: math domain error• Informationsverarbeitung (z. B. Entropie, Datenkompression)
• Komplexitätsanalyse in der Informatik (z. B. bei binären Suchalgorithmen)
• Mathematische Modellierung, z. B. für Schall, Erdbebenstärken, pH-Werte
• Skalierung von Daten im Machine Learning
Für den Logarithmus zur Basis 10 gibt es auch eine eigene Funktion:
math.log10(x)Für den Logarithmus zur Basis 2 ebenfalls:
math.log2(x)log2(x) – Logarithmus zur Basis 2 berechnen
Die Funktion math.log2(x) berechnet den Logarithmus einer Zahl zur Basis 2. Sie ist eine speziell optimierte Variante der allgemeinen math.log(x, 2)-Berechnung.
- Funktionssignatur:
math.log2(x) - Parameter: x: Eine positive Zahl (int oder float)
- Rückgabewert: Gibt den binären Logarithmus von x zurück, also die Potenz, auf die man 2 heben muss, um x zu erhalten. Der Rückgabewert ist vom Typ float.
Bedeutung:
math.log2(x) = log2(x)
Beispiel: log2(8) = 3, denn 23 = 8
import math
wert = 8
ergebnis = math.log2(wert)
print(„log₂(„, wert, „) =“, ergebnis)
print(„log₂(5.5) =“, math.log2(5.5))
• x muss > 0 sein – andernfalls führt der Aufruf zu einem Fehler:
math.log2(0) # ValueErrormath.log2(-3) # ValueError• Informatik & Algorithmik, z. B.
Bedeutung:
math.log10(x) = log10(x)
Beispiel: log10(1000) = 3, denn 103 = 1000
import math
wert = 1000
ergebnis = math.log10(wert)
print(„log₁₀(„, wert, „) =“, ergebnis)
print(„log₁₀(50) =“, math.log10(50))
• Der Wert von x muss größer als 0 sein, sonst wird ein ValueError ausgelöst.
• Wissenschaftliche Berechnungen, z. B. pH-Wert, Erdbebenstärke (Richterskala)
• Datenanalyse und -skalierung, z. B. bei logarithmischer Darstellung von Messwerten
• Ingenieurwesen und Technik, z. B. Schallpegelmessung (Dezibel)
Allgemeine Logarithmusfunktion mit Basis 10 auch möglich durch:
math.log(x, 10)sin(x) – Sinus einer Zahl berechnen
Die Funktion math.sin(x) berechnet den Sinus eines Winkels x, der im Bogenmaß (Radiant) angegeben wird.
- Funktionssignatur:
math.sin(x) - Parameter: x: Ein Winkel in Radiant (float oder int)
- Rückgabewert: Gibt den Sinuswert des Winkels x als Gleitkommazahl (float) zurück.
Der Rückgabewert liegt im Bereich [−1, 1].
Bedeutung:
Der Sinus beschreibt in der Trigonometrie das Verhältnis der Gegenkathete zur Hypotenuse in einem rechtwinkligen Dreieck oder den y-Koordinatenwert auf dem Einheitskreis.
import math
winkel = math.pi / 2
ergebnis = math.sin(winkel)
print(„sin(π/2) =“, ergebnis)
print(„sin(0) =“, math.sin(0))
• Der Winkel x muss in Radiant übergeben werden. Um Grad in Radiant umzuwandeln, kann man
math.radians() verwenden:grad = 90radiant = math.radians(grad)print(math.sin(radiant)) # Ausgabe: 1.0• Mathematische und physikalische Berechnungen
• Signalverarbeitung und Schwingungsanalyse
• Grafikprogrammierung und Animationen
• Trigonometrielösungen bei Geometrie- und Ingenieuraufgaben
cos(x) – Kosinus eines Winkels berechnen
Die Funktion math.cos(x) berechnet den Kosinus eines Winkels x, welcher im Bogenmaß (Radiant) angegeben wird.
- Funktionssignatur:
math.cos(x) - Parameter: x: Winkel in Radiant (float oder int)
- Rückgabewert: Gibt den Kosinuswert des Winkels x als Gleitkommazahl (float) zurück.
Der Rückgabewert liegt im Bereich [−1, 1].
Bedeutung:
Der Kosinus beschreibt in der Trigonometrie das Verhältnis der Ankathete zur Hypotenuse in einem rechtwinkligen Dreieck oder den x-Koordinatenwert auf dem Einheitskreis.
import math
winkel = 0
ergebnis = math.cos(winkel)
print(„cos(0) =“, ergebnis)
print(„cos(π) =“, math.cos(math.pi))
• Der Winkel x muss in Radiant angegeben sein. Zur Umrechnung von Grad in Radiant kann
math.radians() verwendet werden:grad = 180radiant = math.radians(grad)print(math.cos(radiant)) # Ausgabe: -1.0• Berechnung trigonometrischer Funktionen in Mathematik und Physik
• Signalverarbeitung und Wellenanalysen
• Grafische Darstellungen und Animationen
• Lösungen trigonometrischer Gleichungen
tan(x) – Tangens eines Winkels berechnen
Die Funktion math.tan(x) berechnet den Tangens eines Winkels x, wobei der Winkel in Bogenmaß (Radiant) angegeben wird.
- Funktionssignatur:
math.tan(x) - Parameter: x: Winkel in Radiant (float oder int)
- Rückgabewert: Gibt den Tangenswert des Winkels x als Gleitkommazahl (float) zurück.
Der Rückgabewert kann theoretisch jeden reellen Wert annehmen, je nach Winkel.
Bedeutung:
Der Tangens entspricht dem Verhältnis von Sinus zu Kosinus eines Winkels:
tan(x) = sin(x) / cos(x)
import math
winkel = 0
ergebnis = math.tan(winkel)
print(„tan(0) =“, ergebnis)
print(„tan(π/4) =“, math.tan(math.pi / 4))
• Der Winkel x muss in Radiant angegeben werden.
• Der Tangens ist an Stellen undefiniert, an denen der Kosinus null ist (z. B. bei π/2, 3π/2 usw.), was zu sehr großen oder unbestimmten Werten führt.
• Um Grad in Radiant umzuwandeln, kann
math.radians() verwendet werden:grad = 45radiant = math.radians(grad)print(math.tan(radiant)) # Ausgabe: ca. 1.0• Trigonometrische Berechnungen in Mathematik, Physik und Technik
• Geometrische Problemstellungen
• Signal- und Wellenanalyse
• Grafische Programmierung und Animationen
asin(x) – Arkussinus (inverse Sinusfunktion) berechnen
Die Funktion math.asin(x) berechnet den Arkussinus von x, also den Winkel, dessen Sinus x ist. Der Rückgabewert ist ein Winkel im Bogenmaß (Radiant).
- Funktionssignatur:
math.asin(x) - Parameter: x: Ein Wert vom Typ float oder int, der im Bereich [−1, 1] liegen muss.
- Rückgabewert: Gibt den Winkel in Radiant zurück, dessen Sinus den Wert x hat.
Der Rückgabewert liegt im Bereich [−π/2, π/2].
Bedeutung:
Der Arkussinus ist die Umkehrfunktion des Sinus, d.h., für ein gegebenes Verhältnis der Gegenkathete zur Hypotenuse berechnet asin den zugehörigen Winkel.
import math
wert = 1
winkel = math.asin(wert)
print(„asin(1) =“, winkel)
print(„Winkel in Grad:“, math.degrees(winkel))
Winkel in Grad: 90.0
print(„asin(0) =“, math.asin(0))
• Der Eingabewert x muss im Intervall [−1, 1] liegen, sonst löst die Funktion einen ValueError aus.
• Der Rückgabewert ist in Radiant. Zur Umrechnung in Grad kann
math.degrees() genutzt werden.• Berechnung von Winkeln aus trigonometrischen Verhältnissen
• Geometrische und physikalische Anwendungen
• Signal- und Wellenanalysen
• Robotertechnik und Navigation
acos(x) – Arkuskosinus (inverse Kosinusfunktion) berechnen
Die Funktion math.acos(x) berechnet den Arkuskosinus von x, also den Winkel, dessen Kosinus x ist. Der Rückgabewert ist ein Winkel im Bogenmaß (Radiant).
- Funktionssignatur:
math.acos(x) - Parameter: x: Ein Wert vom Typ float oder int, der im Bereich [−1, 1] liegen muss.
- Rückgabewert: Gibt den Winkel in Radiant zurück, dessen Kosinus den Wert x hat.
Der Rückgabewert liegt im Bereich [0, π].
Bedeutung:
Der Arkuskosinus ist die Umkehrfunktion des Kosinus, d.h., für ein gegebenes Verhältnis der Ankathete zur Hypotenuse berechnet acos den zugehörigen Winkel.
import math
wert = 1
winkel = math.acos(wert)
print(„acos(1) =“, winkel)
print(„Winkel in Grad:“, math.degrees(winkel))
Winkel in Grad: 0.0
print(„acos(0) =“, math.acos(0))
print(„Winkel in Grad:“, math.degrees(math.acos(0)))
Winkel in Grad: 90.0
• Der Eingabewert x muss im Intervall [−1, 1] liegen, andernfalls wird ein ValueError ausgelöst.
• Der Rückgabewert ist in Radiant. Zur Umrechnung in Grad kann
math.degrees() verwendet werden.• Berechnung von Winkeln basierend auf trigonometrischen Verhältnissen
• Geometrische Konstruktionen und Analysen
• Physikalische Anwendungen und Simulationen
• Navigation und Robotik
atan(x) – Arkustangens (inverse Tangensfunktion) berechnen
Die Funktion math.atan(x) berechnet den Arkustangens von x, also den Winkel, dessen Tangens x ist. Das Ergebnis ist ein Winkel im Bogenmaß (Radiant).
- Funktionssignatur:
math.atan(x) - Parameter: x: Ein Wert vom Typ float oder int.
- Rückgabewert: Gibt den Winkel in Radiant zurück, dessen Tangens den Wert x hat.
Der Rückgabewert liegt im Bereich [−π/2, π/2].
Bedeutung:
Der Arkustangens ist die Umkehrfunktion des Tangens, d.h., für ein gegebenes Verhältnis von Gegenkathete zu Ankathete berechnet atan den zugehörigen Winkel.
import math
wert = 0
winkel = math.atan(wert)
print(„atan(0) =“, winkel)
print(„Winkel in Grad:“, math.degrees(winkel))
Winkel in Grad: 0.0
print(„atan(1) =“, math.atan(1))
print(„Winkel in Grad:“, math.degrees(math.atan(1)))
Winkel in Grad: 45.0
• Die Eingabe kann jeden reellen Wert annehmen.
• Der Rückgabewert ist in Radiant. Zur Umrechnung in Grad kann
math.degrees() genutzt werden.• Berechnung von Winkeln bei Steigungen oder Verhältnissen
• Geometrische und physikalische Anwendungen
• Navigation und Robotik
• Signal- und Bildverarbeitung
degrees(x) – Umrechnung von Radiant in Grad
Die Funktion math.degrees(x) wandelt einen Winkel von Radiant in Grad um.
- Funktionssignatur:
math.degrees(x) - Parameter: x: Ein Wert vom Typ float oder int, der einen Winkel im Bogenmaß (Radiant) darstellt.
- Rückgabewert: Gibt den entsprechenden Winkel in Grad zurück.
Bedeutung:
Radiant ist die im mathematischen Kontext standardmäßige Einheit für Winkel. Da viele Anwendungen, gerade im Alltag oder in technischen Bereichen, Gradmaß verwenden, ermöglicht degrees() eine einfache Umrechnung.
import math
winkel_radiant = math.pi
winkel_grad = math.degrees(winkel_radiant)
print(„π Radiant sind:“, winkel_grad, „Grad“)
print(„1 Radiant sind:“, math.degrees(1), „Grad“)
• Umrechnung von Winkeln bei trigonometrischen Berechnungen
• Visualisierung und Darstellung von Winkeln in Grad
• Anwendungen in Navigation, Robotik und Geometrie
radians(x) – Umrechnung von Grad in Radiant
Die Funktion math.radians(x) wandelt einen Winkel von Grad in Radiant um.
- Funktionssignatur:
math.radians(x) - Parameter: x: Ein Wert vom Typ float oder int, der einen Winkel im Gradmaß darstellt.
- Rückgabewert: Gibt den entsprechenden Winkel in Radiant zurück.
Bedeutung:
Radiant ist die standardmäßige Einheit für Winkel in der Mathematik und Programmierung. Die Funktion radians() erleichtert die Umrechnung von im Alltag häufig verwendeten Gradmaß in das mathematisch notwendige Bogenmaß.
import math
winkel_grad = 180
winkel_radiant = math.radians(winkel_grad)
print(winkel_grad, „Grad sind:“, winkel_radiant, „Radiant“)
print(„90 Grad sind:“, math.radians(90), „Radiant“)
• Vorbereitung von Winkeln für trigonometrische Funktionen, die Radiant erwarten
• Geometrische und physikalische Berechnungen
• Robotik, Navigation und Simulationen
gcd(x, y) – Größter gemeinsamer Teiler (Greatest Common Divisor)
Die Funktion math.gcd(x, y) berechnet den größten gemeinsamen Teiler (ggT) der beiden ganzzahligen Werte x und y.
- Funktionssignatur:
math.gcd(x, y) - Parameter: x, y: Ganzzahlige Werte vom Typ int.
- Rückgabewert: Gibt den größten gemeinsamen Teiler von x und y als int zurück.
Bedeutung:
Der größte gemeinsame Teiler ist die größte positive ganze Zahl, die sowohl x als auch y ohne Rest teilt. Er wird häufig in der Zahlentheorie, Bruchrechnung und bei der Vereinfachung von Verhältnissen verwendet.
import math
a = 48
b = 18
resultat = math.gcd(a, b)
print(„Der größte gemeinsame Teiler von“, a, „und“, b, „ist:“, resultat)
print(„gcd(7, 13) =“, math.gcd(7, 13))
• Die Funktion akzeptiert auch negative Werte, der ggT wird immer als positiver Wert zurückgegeben.
• Seit Python 3.9 unterstützt
math.gcd auch mehrere Argumente als Tupel.• Mathematische Berechnungen und Algorithmen
• Bruchreduktion und Rationalisierung
• Kryptographie und Zahlentheorie
lcm(x, y) – Kleinstes gemeinsames Vielfaches (Least Common Multiple)
Die Funktion math.lcm(x, y) berechnet das kleinste gemeinsame Vielfache (kgV) der beiden ganzzahligen Werte x und y.
- Funktionssignatur:
math.lcm(x, y) - Parameter: x, y: Ganzzahlige Werte vom Typ int.
- Rückgabewert: Gibt das kleinste gemeinsame Vielfache von x und y als int zurück.
Bedeutung:
Das kleinste gemeinsame Vielfache ist die kleinste positive ganze Zahl, die sowohl durch x als auch durch y ohne Rest teilbar ist. Es wird häufig bei der Addition und Subtraktion von Brüchen sowie in der Zahlentheorie verwendet.
import math
a = 12
b = 15
resultat = math.lcm(a, b)
print(„Das kleinste gemeinsame Vielfache von“, a, „und“, b, „ist:“, resultat)
print(„lcm(7, 13) =“, math.lcm(7, 13))
• Die Funktion akzeptiert auch negative Werte, das Ergebnis ist immer positiv oder null.
• Seit Python 3.9 unterstützt
math.lcm auch mehrere Argumente als Tupel.• Berechnung von gemeinsamen Nennern bei Bruchoperationen
• Mathematische Optimierungen und Algorithmen
• Planung von wiederkehrenden Ereignissen oder Zeitintervallen
Mathematische Konstanten im Modul math
Das Modul math stellt neben zahlreichen Funktionen auch wichtige mathematische Konstanten bereit, die feste Werte enthalten und nicht veränderbar sind.
| Konstante | Bedeutung | Wert |
|---|---|---|
| pi | Kreiszahl (Verhältnis Umfang zu Durchmesser) | 3.141592653589793 |
| e | Eulersche Zahl (Basis des natürlichen Logarithmus) | 2.718281828459045 |
• Konstanten sind spezielle Variablen mit festen, unveränderlichen Werten.
• Sie sind essenziell für mathematische und wissenschaftliche Berechnungen.
• Der Umgang mit Konstanten erleichtert die Programmierung, indem präzise Werte direkt verfügbar sind.
import math
print(„pi =“, math.pi)
print(„e =“, math.e)
e = 2.718281828459045
• Geometrische Berechnungen (Kreis, Kugel, Winkel)
• Exponentielle Wachstumsprozesse
• Naturwissenschaftliche und ingenieurtechnische Anwendungen
Funktionen des Moduls random
Das Modul random ist ein in Python integriertes Modul, das verschiedene Funktionen zur Erzeugung von Zufallszahlen bereitstellt. Im Folgenden wird die wichtigste Funktion erläutert.
random() – Zufallszahl zwischen 0 und 1
Definition:
Die Funktion random.random() liefert eine zufällige Fließkommazahl im Bereich von 0.0 (inklusive) bis 1.0 (exklusive) zurück.
| Merkmal | Beschreibung |
|---|---|
| Funktionsname | random() |
| Parameter | keine |
| Rückgabewert | Zufallszahl float mit 0.0 ≤ N < 1.0 |
import random
print(„Zufallszahl =“, random.random())
print(„Zufallszahl =“, random.random())
print(„Zufallszahl =“, random.random())
Zufallszahl = 0.6932013847210347
Zufallszahl = 0.1584762395871025
Erweiterung des Wertebereichs
Durch einfache mathematische Operationen kann der Wertebereich der Zufallszahlen skaliert werden. Beispielsweise lässt sich die Zahl mit 10 multiplizieren und in einen ganzzahligen Wert umwandeln, um eine Zufallszahl zwischen 0 und 9 zu erhalten.
import random
print(„Zufallszahl =“, int(random.random() * 10))
print(„Zufallszahl =“, int(random.random() * 10))
print(„Zufallszahl =“, int(random.random() * 10))
Zufallszahl = 7
Zufallszahl = 0
•
random.random() ist ideal, um eine Fließkommazahl zwischen 0 und 1 zu erzeugen.• Mittels Multiplikation und Umwandlung lässt sich der Wertebereich flexibel anpassen.
• Diese Funktion bildet die Grundlage für komplexere Zufallszahlgenerierung.
uniform(a, b) – Zufallszahl im Intervall [a, b]
Definition:
Die Funktion random.uniform(a, b) erzeugt eine zufällige Fließkommazahl im Bereich zwischen den beiden angegebenen Grenzen a und b, einschließlich beider Endpunkte.
| Merkmal | Beschreibung |
|---|---|
| Funktionsname | uniform(a, b) |
| Parameter | a (float) – untere Grenze b (float) – obere Grenze |
| Rückgabewert | Zufallszahl float mit a ≤ N ≤ b |
• Die Funktion gibt eine Fließkommazahl zurück, die gleichmäßig verteilt zwischen a und b liegt.
• Die Reihenfolge der Parameter ist flexibel: Wenn a > b ist, wird automatisch der Bereich umgedreht.
• Ideal geeignet, um Zufallswerte in einem beliebigen Intervall zu generieren.
import random
zahl = random.uniform(5.0, 10.0)
print(„Zufallszahl zwischen 5.0 und 10.0:“, zahl)
import random
print(„Zufallszahl zwischen -3.5 und 3.5:“, random.uniform(-3.5, 3.5))
print(„Zufallszahl zwischen 100 und 200:“, random.uniform(100, 200))
print(„Zufallszahl zwischen 10 und 5 (automatische Reihenfolge):“, random.uniform(10, 5))
Zufallszahl zwischen 100 und 200: 156.7834521879503
Zufallszahl zwischen 10 und 5 (automatische Reihenfolge): 6.491027345817234
•
random.uniform(a, b) erzeugt eine zufällige Gleitkommazahl im Intervall a, b.• Parameter
a und b können beliebige reelle Zahlen sein, die Funktion passt sich entsprechend an.• Besonders nützlich bei Simulationen, Spielen oder überall dort, wo Zufallswerte in einem definierten Bereich benötigt werden.
randrange([start,] stop [, step]) – Zufallszahl aus diskretem Bereich
Definition:
Die Funktion random.randrange() erzeugt eine zufällige Ganzzahl aus einem diskreten Bereich, der durch Start-, Stopp- und Schrittwerte definiert wird. Die Werte liegen im halb-offenen Intervall [start, stop), also inklusive start, aber exklusive stop.
| Merkmal | Beschreibung |
|---|---|
| Funktionsname | randrange([start,] stop [, step]) |
| Parameter | start (optional, int) – untere Grenze (inklusive), Standard: 0 stop (int) – obere Grenze (exklusive) step (optional, int) – Schrittweite, Standard: 1 |
| Rückgabewert | Zufällige Ganzzahl aus dem Bereich [start, stop) mit Schritt step |
start, start + step, start + 2*step, …, bis aber kleiner als stop
•
stop ist exklusiv: die Zahl stop selbst wird nicht zurückgegeben.• Wenn
step größer als 1 ist, werden nur Werte in den angegebenen Schritten ausgewählt.• Falls
start nicht angegeben ist, beginnt der Bereich bei 0.• Die Funktion eignet sich besonders, um Zufallszahlen aus einer definierten Teilmenge von ganzen Zahlen zu erzeugen.
import random
zahl = random.randrange(10) # Bereich: 0 bis 9
print(„Zufallszahl zwischen 0 und 9:“, zahl)
import random
zahl = random.randrange(5, 20) # Bereich: 5 bis 19
print(„Zufallszahl zwischen 5 und 19:“, zahl)
import random
zahl = random.randrange(10, 50, 5) # Bereich: 10, 15, 20, …, 45
print(„Zufallszahl zwischen 10 und 45 in 5er-Schritten:“, zahl)
•
randrange() wirft einen Fehler, wenn kein gültiger Bereich existiert (z. B. wenn start >= stop oder wenn step 0 ist).•
randrange() ist besonders nützlich bei der Erzeugung von Zufallszahlen mit bestimmten Intervallen, z. B. für Simulationen, Spiele oder Sampling.•
randrange() generiert eine zufällige ganze Zahl aus einer diskreten Folge.• Standardmäßig beginnt der Bereich bei 0, kann aber mit
start angepasst werden.• Der obere Grenzwert
stop ist immer exklusiv.• Die Schrittweite
step ermöglicht flexible Auswahl nur bestimmter Werte innerhalb des Bereichs.• Besonders praktisch bei zufälliger Auswahl aus einer Menge von Zahlen mit festen Abständen.
choice(seq) – Zufällige Auswahl eines Elements aus einer Sequenz
Beschreibung:
Die Funktion random.choice() dient der zufälligen Auswahl eines einzelnen Elements aus einer nicht-leeren Sequenz. Die übergebene Sequenz kann dabei eine Liste, ein Tupel, ein String oder eine andere sequentielle Datenstruktur sein.
- Parameter: seq (Sequenz): Eine nicht-leere Folge von Elementen, aus der ein einzelnes Element zufällig ausgewählt wird.
Die Funktion erwartet, dass die Sequenz mindestens ein Element enthält; andernfalls wird ein IndexError ausgelöst. - Rückgabewert: Gibt ein zufällig ausgewähltes Element aus der angegebenen Sequenz zurück.
• Auswahl erfolgt mit gleichverteilter Wahrscheinlichkeit für alle Elemente.
• Keine Modifikation der Eingabesequenz.
import random
farben = [‚Rot‘, ‚Grün‘, ‚Blau‘, ‚Gelb‘, ‚Schwarz‘]
zufallselement = random.choice(farben)
print(„Ausgewählte Farbe:“, zufallselement)
import random
text = „Python“
zufallszeichen = random.choice(text)
print(„Zufällig ausgewähltes Zeichen:“, zufallszeichen)
import random
zahlen = (11, 22, 33, 44, 55)
auswahl = random.choice(zahlen)
print(„Zufällig ausgewählte Zahl:“, auswahl)
• Auswahl zufälliger Optionen, etwa bei Spielen oder Entscheidungsfindungen.
• Sampling aus diskreten Datenmengen.
• Implementierung von Algorithmen, die zufällige Auswahl benötigen, wie z. B. beim Testen oder bei Simulationen.
shuffle(x) – Zufälliges Mischen einer Liste
Beschreibung:
Die Funktion random.shuffle() dient dazu, die Elemente einer veränderbaren Sequenz (z. B. einer Liste) zufällig und in-place neu anzuordnen. Das bedeutet, dass die Reihenfolge der Elemente innerhalb der Originalsequenz direkt geändert wird, ohne eine neue Liste zu erzeugen.
- Parameter: x (veränderbare Sequenz): Eine Sequenz vom Typ list (oder eine andere mutable Sequenz), deren Elemente zufällig permutiert (durchmischt) werden sollen.
- Rückgabewert: Die Funktion gibt
Nonezurück, da sie die übergebene Sequenz direkt modifiziert.
• Die Anordnung der Elemente in der Liste wird zufällig und gleichverteilt geändert.
• Funktioniert nur mit veränderbaren Sequenztypen, z. B. Listen.
• Für unveränderliche Sequenzen (wie Tupel oder Strings) ist shuffle nicht anwendbar.
import random
zahlen = [1, 2, 3, 4, 5]
print(„Original:“, zahlen)
random.shuffle(zahlen)
print(„Gemischt:“, zahlen)
Gemischt: [3, 1, 5, 2, 4]
import random
teilnehmer = [‚Anna‘, ‚Ben‘, ‚Clara‘, ‚David‘, ‚Eva‘]
print(„Ursprüngliche Reihenfolge:“, teilnehmer)
random.shuffle(teilnehmer)
print(„Neue Reihenfolge:“, teilnehmer)
Neue Reihenfolge: [‚Eva‘, ‚Clara‘, ‚Ben‘, ‚Anna‘, ‚David‘]
shuffle() die Originalsequenz ändert, sollte man ggf. vor der Anwendung eine Kopie erstellen, wenn die ursprüngliche Reihenfolge erhalten bleiben soll:import randomoriginal = [10, 20, 30, 40]kopie = original[:]random.shuffle(kopie)print("Original:", original)print("Gemischt:", kopie)• Spiele und Simulationen, in denen zufällige Reihenfolgen benötigt werden.
• Zufällige Anordnung von Elementen für Tests oder Experimente.
• Shuffling von Karten, Listen oder Teilnehmern in verschiedenen Kontexten.
Lektion 9: Der Umgang mit Texten
1. Das Konzept der Texte
Ein Text ist eine Reihe von Zeichen ohne eine festgelegte Größe, er kann aus einem Zeichen, einem Wort, einem Satz oder einem sehr großen Absatz bestehen. In Python gehört der Text zum Typ str. In dieser Lektion werden Sie alle Möglichkeiten kennenlernen, wie Sie Text definieren können, sowie die bereitgestellten Funktionen, die Sie verwenden können, um Texte zu bearbeiten, in ihnen zu suchen und sie zu zerschneiden. Der Typ str basiert auf der UTF-8 Kodierung, was bedeutet, dass Sie keine Probleme beim Arbeiten mit arabischen, englischen, französischen usw. Texten haben werden.
2. Methode zur Definition eines Textes
' '), doppelte (" ") oder dreifache (''' ''' oder """ """) Anführungszeichen verwenden. Strings sind unveränderlich (immutable).
# Enthält einen Textwert mit einfachen und doppelten Anführungszeichen
text = """ In dieser Zeile drucken wir 'einfache Anführungszeichen'.
In dieser Zeile drucken wir "doppelte Anführungszeichen." """
print(text)
In dieser Zeile drucken wir „doppelte Anführungszeichen.“
3. Texte zusammenführen
Die Verkettung bedeutet, eine Reihe von Dingen nebeneinander zu setzen, damit sie zu einem einzigen Text werden. Sie können Text mit Text und Text mit Zahlen verbinden. Es gibt mehrere Methoden:
- Automatische Verkettung, wenn zwei Textwerte direkt nebeneinander stehen
- Verwendung des Operators
+(Text + Text oder Text + Zahl) - Verwendung der Funktion
join()für Listen von Strings
# Beispiel: Vorname und Nachname zusammenfügen
vorname = 'Mark'
nachname = vollständiger_name = vorname + nachname
print(vollständiger_name)
# Automatische Verkettung durch direktes Aneinanderreihen
vollständiger_name = 'Mark' ' Mueller'
print(vollständiger_name)
# join()-Methode für Listen von Strings
namen = ['Max', 'Mustermann', 'Musterfirma']
verbundene_namen = ", ".join(namen)
print('Verbundene Namen: ' + verbundene_namen)
4. Zugriff auf die Textzeichen
Angenommen, wir definieren eine Variable text mit dem Inhalt:
text = 'Python macht Spaß!'
Dieser Text wird im Speicher zeichenweise und in der richtigen Reihenfolge abgelegt. Jedes Zeichen erhält dabei einen Index, der entweder vorwärts (von links nach rechts) oder rückwärts (von rechts nach links) gezählt wird.
Die Indizes beginnen bei 0 und laufen von links nach rechts:
| Zeichen | P | y | t | h | o | n | m | a | c | h | t | S | p | a | ß | ! | ||
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
# Zugriff auf einzelne Zeichen (vorwärts)
text = 'Python macht Spaß!'
print(text[0] + text[1] + text[2] + text[3] + text[4] + text[5])
# Kürzer mit Slicing
print(text[0:6])
# Zugriff auf Zeichen von rechts (negativer Index)
print(text[-5] + text[-4] + text[-3] + text[-2] + text[-1])
# Slicing von rechts
print(text[-5:])
# Beispiel: Die letzten 4 Zeichen ausgeben (→ "Spaß!")
text = 'Python macht Spaß!'
print(text[-5] + text[-4] + text[-3] + text[-2] + text[-1])
print(text[-5:])
# Länge eines Strings ermitteln
text = 'Python macht Spaß!'
print('Anzahl der Zeichen:', len(text))
| Begriff | Erklärung |
|---|---|
| Length | Länge des Strings (Zeichenanzahl) |
| Index | Position eines Zeichens |
| Indices | Mehrzahl von Index |
| Substring | Ein Teilbereich des Strings |
5. Slicing – Teilbereiche aus dem String holen
Mit der Syntax text[start:ende] kannst du Teile des Strings extrahieren.
# Beispiel 1: Von Zeichen 7 bis 11 (→ "macht")
text = 'Python macht Spaß!'
print(text[7:12])
# Beispiel 2: Von Index 7 bis zum Ende (→ "macht Spaß!")
print(text[7:])
# Beispiel 3: Vom Anfang bis Index 6 (→ "Python")
print(text[:6])
print(text[0:6])Python erlaubt auch negative Indizes:
| Zeichen | P | y | t | h | o | n | m | a | c | h | t | S | p | a | ß | ! | ||
| Index | -18 | -17 | -16 | -15 | -14 | -13 | -12 | -11 | -10 | -9 | -8 | -7 | -6 | -5 | -4 | -3 | -2 | -1
5. Zeilenumbrüche und Steuerzeichen
Zeilenumbrüche werden durch spezielle Steuerzeichen erzeugt:
| Zeichen | Beschreibung |
|---|---|
\n | Neue Zeile (Unix, Linux, macOS) |
\r | Wagenrücklauf (ältere Macs) |
\r\n | Kombination (Windows) |
| Weitere | \v, \f, \x1c, \u2028 usw. für spezielle Trennungen |
# Beispiel: Mehrzeiliger Text with \n
text = 'Zeile 1\nZeile 2\nZeile 3'
print(text)
Zeile 2
Zeile 3
\n selbst wird nicht angezeigt, es bewirkt lediglich den Umbruch zur nächsten Zeile.✅ Zusätzliche individuelle Beispiele
# Rückwärts ausgeben
print(text[::-1])
# Ein Wort extrahieren
wort = 'Programmieren'
print(wort[0:11]) # Gibt 'Programmier' zurück
7. Die fertigen Funktionen in der Klasse str
Die str-Klasse in Python bietet eine Vielzahl an Methoden, um mit Zeichenketten effizient zu arbeiten. In dieser professionellen Lektion werden alle Methoden der str-Klasse systematisch in fünf Kategorien erklärt:
- Suchmethoden (Searching)
- Teilung & Extraktion (Substring/Splitting)
- Ersetzungsmethoden (Replacing)
- Verarbeitungsmethoden (Manipulation)
- Vergleichsmethoden (Comparison)
Jede Methode wird einzeln mit mindestens drei Beispielen, technischen Hinweisen und nützlichen Anwendungsfällen vorgestellt.
Suchmethoden (Searching)
count(sub[, start[, end]]) Zählt, wie oft ein bestimmter Teilstring in der Zeichenkette vorkommt. Optional kann über start und end ein Bereich angegeben werden, in dem gezählt wird (wie bei einem Slice [start:end]).
text = "banana"
print(text.count("a")) # Ausgabe: 3
print(text.count("na")) # Ausgabe: 2
print(text.count("a", 2, 5)) # Ausgabe: 1
- Gibt 0 zurück, wenn der gesuchte Teilstring nicht vorhanden ist.
- Die Zählung beginnt bei
start(inkl.) und endet vorend(exkl.). - Überlappende Teilstrings werden nicht gezählt.
Beispiel:→ nicht 2, da „aa“ nur einmal ohne Überlappung gezählt wirdtext = "aaa" print(text.count("aa")) # Ausgabe: 1 - Anwendungsfall: Zählen von Schlüsselwörtern, Buchstaben oder Mustern in Daten.
find(sub[, start[, end]]) Gibt den Index der ersten Übereinstimmung des Teilstrings sub zurück oder -1, wenn sub nicht gefunden wird. Optional kann der Suchbereich über start und end eingeschränkt werden.
text = "programming"
print(text.find("g")) # Ausgabe: 3
print(text.find("m")) # Ausgabe: 6
print(text.find("z")) # Ausgabe: -1
startundendbegrenzen den Bereich der Suche.- Gibt den kleinsten Index zurück, an dem
subgefunden wird. - Anwendungsfall: Nützlich zur Prüfung, ob ein Substring existiert, ohne Fehler auszulösen.
rfind(sub[, start[, end]]) Wie find(), aber liefert den größten Index, bei dem sub gefunden wird – also wird von rechts nach links gesucht, obwohl der Index von links gezählt wird.
text = "banana"
print(text.rfind("a")) # Ausgabe: 5
print(text.rfind("na")) # Ausgabe: 4
print(text.rfind("x")) # Ausgabe: -1
- Praktisch, um das letzte Vorkommen eines Teilstrings zu lokalisieren.
index(sub[, start[, end]]) Wie find(), aber anstelle von -1 wird ein ValueError ausgelöst, wenn der Teilstring nicht gefunden wird.
text = "hello world"
print(text.index("world")) # Ausgabe: 6
print(text.index("o")) # Ausgabe: 4
# print(text.index("z")) # ValueError
- Für kontrolliertes Fehlerhandling nützlich, wenn das Fehlen des Substrings als Fehlerfall gewertet wird.
rindex(sub[, start[, end]]) Wie rfind(), aber gibt ebenfalls einen ValueError zurück, wenn der Teilstring nicht gefunden wird.
text = "banana"
print(text.rindex("a")) # Ausgabe: 5
print(text.rindex("na")) # Ausgabe: 4
# print(text.rindex("z")) # ValueError
Teilung & Extraktion (Substring/Splitting)
split(sep=None, maxsplit=-1) Teilt eine Zeichenkette anhand eines Trennzeichens (sep) in eine Liste von Teilstrings.
Funktionsweise:
- sep: Das Zeichen oder der Teilstring, an dem die Trennung erfolgt. Standardmäßig ist
sep=None, was bedeutet, dass die Zeichenkette an beliebigen Whitespaces (Leerzeichen, Tabs, Zeilenumbrüche) getrennt wird – zusammenhängende Whitespaces gelten als ein Trenner. - maxsplit: Gibt die maximale Anzahl an Trennungen an. Standardwert -1 bedeutet, dass alle möglichen Trennungen durchgeführt werden.
text = "one,two,three"
print(text.split(",")) # ['one', 'two', 'three']
print(text.split(",", 1)) # ['one', 'two,three']
print("a b c\td".split()) # ['a', 'b', 'c', 'd']
- Bei Verwendung von
sep=Noneentfernt Python automatisch führende und nachfolgende Whitespaces. - Bei festem
sepwird exakt nach diesem Teilstring getrennt – mehrere direkt aufeinanderfolgende Vorkommen führen zu leeren Strings in der Liste:
print("apple;;banana;cherry".split(";")) # ['apple', '', 'banana', 'cherry'] maxsplitwirkt sich von links nach rechts aus. Nach dem Erreichen der maxsplit-Grenze bleibt der Rest der Zeichenkette unverändert:
text = "a,b,c,d" print(text.split(",", 2)) # ['a', 'b', 'c,d']- Anwendungsfälle: CSV-Verarbeitung, Parsen von Protokollen, Normalisierung von Eingaben.
rsplit(sep=None, maxsplit=-1) Wie split(), aber die Teilung erfolgt von rechts nach links.
Besonders nützlich, wenn man z.B. nur das letzte Vorkommen eines Trenners berücksichtigen möchte.
text = "apple,banana,cherry"
print(text.rsplit(",", 1)) # ['apple,banana', 'cherry']
print(text.rsplit(",", 2)) # ['apple', 'banana', 'cherry']
print(" a b c d ".rsplit()) # ['a', 'b', 'c', 'd']
partition(sep) Teilt die Zeichenkette genau einmal an der ersten Stelle, an der sep auftaucht.
Gibt ein 3-Tupel zurück: (Teil vor sep, sep selbst, Teil nach sep).
Wenn sep nicht gefunden wird, ist der Rückgabewert (ganze Zeichenkette, “, “).
text = "apple-banana-cherry"
print(text.partition("-")) # ('apple', '-', 'banana-cherry')
print(text.partition(",")) # ('apple-banana-cherry', '', '')
print("hello world".partition(" ")) # ('hello', ' ', 'world')
- Nur der erste Fund wird verwendet.
- Praktisch für einfache, einmalige Trennungen, z. B. bei Key-Value-Paaren.
rpartition(sep) Wie partition(), aber teilt an der letzten Stelle von sep.
Gibt ebenfalls ein 3-Tupel zurück: (Teil vor sep, sep selbst, Teil nach sep).
Wenn sep nicht gefunden wird, ist das Ergebnis ('', '', ganze Zeichenkette).
text = "apple-banana-cherry"
print(text.rpartition("-")) # ('apple-banana', '-', 'cherry')
print(text.rpartition(",")) # ('', '', 'apple-banana-cherry')
print("hello world world".rpartition(" ")) # ('hello world', ' ', 'world')
Slice-Operator (
text[start:end])Obwohl kein Methodenaufruf, ist das Substring-Extrahieren über Slicing fundamental:
- start ist inklusiv, end exklusiv.
- Negative Indizes zählen vom Ende der Zeichenkette rückwärts.
text = "programming"
print(text[0:6]) # 'progra'
print(text[3:]) # 'gramming'
print(text[-3:]) # 'ing'
print(text[:4]) # 'prog'
- Bei nicht gesetztem
startoderendwird vom Anfang bzw. bis zum Ende genommen. - Nützlich für Extraktion fester oder variabler Substrings.
startswith(prefix[, start[, end]]) & endswith(suffix[, start[, end]]) Diese Methoden prüfen, ob die Zeichenkette an einer bestimmten Stelle mit einem Präfix oder Suffix beginnt oder endet.
Optional können Bereiche durch start und end definiert werden.
text = "hello world"
print(text.startswith("hell")) # True
print(text.startswith("world", 6)) # True
print(text.endswith("world")) # True
print(text.endswith("hello")) # False
print(text.endswith("wor", 0, 8)) # True
- Essentiell, um Strings in Python präzise und effizient zu zerlegen und zu extrahieren.
- Werden oft zusammen mit weiteren Methoden wie
strip,replace,findgenutzt.
Ersetzungsmethoden (Replacing)
replace(old, new[, count]) Ersetzt alle Vorkommen eines Teilstrings old durch einen neuen Teilstring new.
- old: Der zu ersetzende Teilstring.
- new: Der neue Teilstring.
- count: Optional, gibt an, wie viele Ersetzungen maximal durchgeführt werden. Standard ist -1 (alle Vorkommen).
text = "banana"
print(text.replace("a", "o")) # 'bonono'
print(text.replace("na", "NA")) # 'baNANA'
print(text.replace("a", "o", 2)) # 'bonona'
replace()gibt eine neue Zeichenkette zurück, da Strings in Python unveränderlich sind.- Wenn
oldnicht gefunden wird, bleibt der String unverändert. - Sehr nützlich zum Korrigieren, Anpassen oder Filtern von Text.
translate(table) Ersetzt Zeichen anhand einer Übersetzungstabelle, die z.B. mit str.maketrans() erzeugt wird.
- table ist ein Mapping von Unicode-Codepunkten (int) oder Zeichen zu neuen Zeichen oder
None(zum Löschen). - Besonders effizient, wenn viele unterschiedliche Zeichen ersetzt oder gelöscht werden sollen.
text = "hello world"
table = str.maketrans("hw", "HW")
print(text.translate(table)) # 'Hello World'
# Löschen von Zeichen: Ersetze 'l' durch None (löschen)
table_del = str.maketrans("", "", "l")
print(text.translate(table_del)) # 'heo word'
translate()ersetzt einzelne Zeichen, nicht Substrings.- Sehr performant bei vielen Zeichenersetzungen.
removeprefix(prefix) Entfernt ein gegebenes Präfix prefix vom Anfang der Zeichenkette, falls vorhanden.
Gibt die Originalzeichenkette zurück, wenn das Präfix nicht vorhanden ist.
Seit Python 3.9 verfügbar.
text = "unhappy"
print(text.removeprefix("un")) # 'happy'
print(text.removeprefix("in")) # 'unhappy'
print("prefix_string".removeprefix("prefix_")) # 'string'
- Praktisch, um z.B. fest definierte Präfixe elegant zu entfernen.
removesuffix(suffix) Entfernt ein gegebenes Suffix suffix vom Ende der Zeichenkette, falls vorhanden.
Gibt die Originalzeichenkette zurück, wenn das Suffix nicht vorhanden ist.
Seit Python 3.9 verfügbar.
filename = "report.pdf"
print(filename.removesuffix(".pdf")) # 'report'
print(filename.removesuffix(".txt")) # 'report.pdf'
print("filename_backup".removesuffix("_backup")) # 'filename'
- Ideal zum Entfernen von Dateiendungen oder ähnlichen festen Endungen.
Kombinationen und Anwendungsfälle
filename = "temp_report_backup.pdf"
clean_name = filename.removeprefix("temp_").removesuffix("_backup.pdf")
print(clean_name) # 'report'
str.maketrans(x[, y[, z]]) Erzeugt eine Übersetzungstabelle für die Methode translate().
- x und y müssen gleich lang sein, wenn beide angegeben sind. Jedes Zeichen aus x wird durch das entsprechende Zeichen aus y ersetzt.
- z ist eine optionale Zeichenkette, deren Zeichen beim Übersetzen gelöscht werden sollen.
maketrans() liefert eine Mapping-Tabelle, die translate() verwendet, um einzelne Zeichen zu ersetzen oder zu löschen. Es ist eine statische Methode, die auf str aufgerufen wird: str.maketrans(...).
# Beispiel 1: Zeichen ersetzen
table = str.maketrans("abc", "123")
print("abcde".translate(table)) # '123de'
# Beispiel 2: Zeichen löschen (über 'z')
table = str.maketrans("", "", "xyz")
print("xyzabcxyz".translate(table)) # 'abc'
# Beispiel 3: Kombination aus Ersetzen und Löschen
table = str.maketrans("aeiou", "12345", "xyz")
print("example xyz".translate(table)) # '2x1mpl '
- Wird meist zusammen mit
translate()verwendet, um große Mengen von Zeichen schnell zu ersetzen oder zu entfernen. - Effizienter als mehrfaches
replace()bei vielen Ersetzungen. - Nützlich für z.B. einfache Verschlüsselungen, Filterung von Zeichen oder Zeichensatzkonvertierungen.
center(width[, fillchar]) Zentriert die Zeichenkette in einem Feld der Breite width. Das Füllzeichen fillchar ist optional (Standard: Leerzeichen).
text = "hello"
print(text.center(11)) # " hello "
print(text.center(11, "*")) # "***hello***"
ljust(width[, fillchar])Linksbündige Ausrichtung mit optionalem Füllzeichen.
text = "hello"
print(text.ljust(10)) # "hello "
print(text.ljust(10, "-")) # "hello-----"
rjust(width[, fillchar])Rechtsbündige Ausrichtung mit optionalem Füllzeichen.
text = "hello"
print(text.rjust(10)) # " hello"
print(text.rjust(10, "-")) # "-----hello"
zfill(width) Füllt die Zeichenkette von links mit Nullen auf, bis die Länge width erreicht ist. Nützlich für Zahlenformatierungen.
text = "42"
print(text.zfill(5)) # "00042"
text = "-42"
print(text.zfill(5)) # "-0042"
expandtabs(tabsize=8) Ersetzt Tabulatoren (\t) durch Leerzeichen, wobei die Tabulatorenstellung alle tabsize Zeichen ausgerichtet wird.
text = "a\tb\tc"
print(text.expandtabs()) # "a b c"
print(text.expandtabs(4)) # "a b c"
- strip, lstrip, rstrip: Praktisch zur Eingabebereinigung.
- lower, upper, capitalize, title, swapcase: Zur Normalisierung von Texten, z. B. für Vergleiche oder Formatierungen.
- replace: Textmodifikation, z. B. Ersetzen von Sonderzeichen, URLs, oder Tokens.
- center, ljust, rjust, zfill: Für die Textformatierung, Ausgabe in Tabellen, Nummernformate.
- expandtabs: Umwandlung von Tabulatoren in Leerzeichen für einheitliche Darstellung.
Vergleichsmethoden (Comparison)
Diese Methoden prüfen bestimmte Eigenschaften oder Beziehungen einer Zeichenkette und liefern als Ergebnis stets einen Wahrheitswert (True oder False). Sie werden häufig für Validierungen, Filter oder bedingte Logik eingesetzt.
startswith(prefix[, start[, end]]) Prüft, ob die Zeichenkette mit dem angegebenen Präfix beginnt. Optional können Teilbereiche der Zeichenkette betrachtet werden (von start bis end).
text = "Hello World"
print(text.startswith("Hello")) # True
print(text.startswith("World")) # False
print(text.startswith("World", 6)) # True
print(text.startswith(("Hi", "He"))) # True
endswith(suffix[, start[, end]])Prüft, ob die Zeichenkette mit dem angegebenen Suffix endet. Ebenso können Start- und Endpositionen angegeben werden.
filename = "report.pdf"
print(filename.endswith(".pdf")) # True
print(filename.endswith(".doc")) # False
print(filename.endswith("port.pdf", 0)) # True
print(filename.endswith((".jpg", ".pdf"))) # True
isalpha()Prüft, ob alle Zeichen Buchstaben sind (keine Leerzeichen, Zahlen oder Sonderzeichen).
print("Hallo".isalpha()) # True
print("Hallo123".isalpha()) # False
print("Hallo Welt".isalpha()) # False
isdigit()Prüft, ob alle Zeichen Ziffern sind (0–9).
print("12345".isdigit()) # True
print("12a45".isdigit()) # False
print("²³".isdigit()) # True
isnumeric()Prüft, ob alle Zeichen numerisch sind. Dies umfasst nicht nur Ziffern (0–9), sondern auch andere Unicode-Zahlen wie Brüche, hochgestellte Zahlen, römische Zahlen etc.
print("12345".isnumeric()) # True
print("½".isnumeric()) # True (Unicode-Bruch)
print("²³".isnumeric()) # True (hochgestellte Zahlen)
print("12a45".isnumeric()) # False
print("123 456".isnumeric()) # False (Leerzeichen)
isdigit():isdigit() prüft auf Ziffern (Digits), während isnumeric() einen erweiterten Bereich von numerischen Zeichen einschließt, z.B. auch Unicode-Zahlen, die keine Ziffern im engeren Sinne sind.isspace()Prüft, ob alle Zeichen Whitespaces sind (Leerzeichen, Tabs, Zeilenumbrüche).
print(" \t\n".isspace()) # True
print(" a ".isspace()) # False
print("".isspace()) # False (leere Zeichenkette)
islower()Prüft, ob alle Buchstaben in Kleinbuchstaben sind. Nicht-Buchstaben werden ignoriert.
print("hello".islower()) # True
print("Hello".islower()) # False
print("1234".islower()) # False (keine Buchstaben)
print("hello123".islower()) # True
isupper()Prüft, ob alle Buchstaben in Großbuchstaben sind. Nicht-Buchstaben werden ignoriert.
print("HELLO".isupper()) # True
print("Hello".isupper()) # False
print("1234".isupper()) # False (keine Buchstaben)
print("HELLO123".isupper()) # True
istitle()Prüft, ob jedes Wort mit einem Großbuchstaben beginnt, gefolgt von Kleinbuchstaben.
print("Hello World".istitle()) # True
print("Hello world".istitle()) # False
print("123 Hello".istitle()) # True
casefold()Ist keine Vergleichsmethode, sondern erzeugt eine stark normalisierte, kleingeschriebene Version der Zeichenkette, die für case-insensitive Vergleiche empfohlen wird.
a = "straße"
b = "STRASSE"
print(a.casefold() == b.casefold()) # True (übliche lower() nicht ausreichend)
Vergleichsoperatoren:
==, !=, <, >, <=, >=Neben den Methoden sind auch die eingebauten Vergleichsoperatoren elementar für String-Vergleiche, die lexikographisch (alphabetisch) durchgeführt werden.
print("abc" == "abc") # True
print("abc" != "def") # True
print("abc" < "bcd") # True (lexikographisch)
print("abc" > "abd") # False
- Präfix-/Suffix-Checks: Für Filter von Dateinamen, URLs, Eingaben.
- Typprüfungen: Validierung von Benutzereingaben, z. B. ob nur Zahlen enthalten sind.
- Groß-/Kleinschreibung: Für Normalisierung und korrekte Formatprüfungen.
- Lexikographische Vergleiche: Sortierungen, Suchalgorithmen, Bedingungen.
% (Formatierung) Der %-Operator wird zur Formatierung von Strings verwendet. Dabei kann man Platzhalter definieren, die dann durch Werte ersetzt werden.
%sfür Strings%dfür ganze Zahlen (Integers)%ffür Fließkommazahlen (Floats)
name = "Sarah"
alter = 25
kontostand = 1234.56
print("Mein Name ist %s." % name)
print("Ich bin %d Jahre alt." % alter)
print("Mein Kontostand beträgt %.2f Euro." % kontostand)
Ich bin 25 Jahre alt.
Mein Kontostand beträgt 1234.56 Euro.
| Ausdruck | Bedeutung |
|---|---|
%s | Platzhalter für Strings. → „Sarah“ wird an die Stelle von %s eingefügt. |
%d | Platzhalter für ganze Zahlen (Integer). → 25 ersetzt %d. |
%.2f | Platzhalter für Fließkommazahlen (Float) mit 2 Nachkommastellen. → 1234.56 ersetzt %.2f. |
- Lesbarkeit: Platzhalter verbessern die Struktur.
- Flexibilität: Daten können dynamisch ersetzt werden.
- Kompatibel mit älterem Python-Code (besonders vor Python 3.6).
Operator
in (Überprüfung auf Teilstring) Der in-Operator überprüft, ob ein bestimmter Teilstring in einem String enthalten ist. Er liefert True zurück, wenn der Teilstring gefunden wird, sonst False.
text = 'Python ist leicht zu lernen.'
print('leicht' in text) # True
print('schwer' in text) # False
False
'leicht' im String text vorkommt, gibt in True zurück. Für 'schwer' wird False zurückgegeben, da es nicht enthalten ist.Operator
not in (Überprüfung auf Nichtvorhandensein) Der not in-Operator überprüft, ob ein bestimmter Teilstring nicht in einem String enthalten ist. Er liefert True zurück, wenn der Teilstring nicht gefunden wird, sonst False.
text = 'Python ist leicht zu lernen.'
print('leicht' not in text) # False
print('schwer' not in text) # True
True
'leicht' in text enthalten ist, ergibt not in False. Für 'schwer' (nicht enthalten) ergibt sich True.Zusammenfassung
| Operator | Funktion | Beispiel | Ergebnis |
|---|---|---|---|
+ | Verkettung von Strings | 'Hallo ' + 'Welt' | 'Hallo Welt' |
* | Wiederholung eines Strings | 'Hi! ' * 3 | 'Hi! Hi! Hi! ' |
% | String-Formatierung mit Platzhaltern | 'Name: %s, Alter: %d' % ('Anna', 25) | 'Name: Anna, Alter: 25' |
in | Prüfen, ob Teilstring enthalten | 'lo' in 'Hallo' | True |
not in | Prüfen, ob Teilstring nicht enthalten | 'xy' not in 'Hallo' | True |