Einleitung: Warum Logik im Code essenziell ist?
Logik ist das Fundament jeder Software. Ob in Webseiten, Apps oder komplexen Systemen – Entscheidungen, Schleifen, Verzweigungen und Fehlerbehandlungen beruhen auf logischen Ausdrücken. Ohne eine strukturierte Logik wären Programme chaotisch, fehleranfällig und schwer wartbar.
Stell dir vor, du willst eine Bedingung in deinem Programm prüfen. Ist es viel einfacher, das mit einer klaren Logik zu machen? Genau das macht Logik in der Programmierung unverzichtbar. Sie hilft dir, Entscheidungen im Code zu treffen, Fakten zu kombinieren und komplexe Abläufe zu steuern.
Ein zentrales Werkzeug zur Umsetzung dieser Logik sind boolesche Ausdrücke. Diese operieren mit zwei Zuständen: wahr (true) und falsch (false). Mithilfe von Truth Tables (Wahrheitstabellen) lassen sich diese Ausdrücke visuell analysieren, testen und optimieren. Ziel dieses Beitrags ist es, die Grundlagen, Anwendungen und Optimierungen boolescher Logik im Detail zu erklären, inklusive praxisnaher Beispiele und Übungsaufgaben mit Lösungen.
Inhalt
- Einleitung: Warum Logik im Code essenziell ist
- 1. Grundkonzepte der Booleschen Logik
- 2. Logische Operatoren und ihre Bedeutung
- 3. Grundlagen der booleschen Algebra
- 4. Truth Tables: Das Werkzeug zur Visualisierung logischer Zusammenhänge
- 5. Boolesche Ausdrücke im Code umsetzen
- 6. Anwendungsbeispiele aus der Praxis
- 7. Aufgaben zur Vertiefung
- 8. Optimierung von logischen Ausdrücken
- 9. Fallstudie: Logik in der echten Softwareentwicklung
- 10. Erweiterte Themen und zukünftige Trends
- 11. Herausforderungen und offene Fragen
- Fazit
1. Grundkonzepte der Booleschen Logik
1.1. Was sind Boolesche Ausdrücke?
Boolesche Ausdrücke bestehen aus Variablen, die nur zwei Werte haben können: true oder false. Diese Variablen heißen Boolesche Variablen. Man braucht sie, um Bedingungen zu prüfen. Zum Beispiel: „Ist die Zahl größer als 10?“ – das ist eine boolesche Frage. Im Alltag könnten wir sagen: „Bin ich wach?“ – ja oder nein.
In Programmen sind boolesche Ausdrücke einfache Wahrheitsprüfungen. Sie helfen bei Entscheidungen und steuern den Ablauf des Programms. Man kann sie zu komplexeren Ausdrücken kombinieren, um mehr Bedingungen zu prüfen.
Ein boolescher Ausdruck ist eine logische Aussage, die entweder den Wert true (wahr) oder false (falsch) ergibt. Solche Ausdrücke werden verwendet, um Bedingungen zu prüfen und Entscheidungen im Programm zu steuern.
Beispiel (Python):
is_logged_in = True
has_admin_rights = False
if is_logged_in and has_admin_rights:
print("Zugang erlaubt")
else:
print("Zugang verweigert")Hier besteht der boolesche Ausdruck aus zwei Variablen: is_logged_in und has_admin_rights. Beide müssen True sein, damit der Nutzer Zugriff erhält.
2. Logische Operatoren und ihre Bedeutung
In der booleschen Logik verwendet man verschiedene Operatoren, um Ausdrücke zu kombinieren. Diese Operatoren funktionieren gleich, unabhängig von der Programmiersprache, auch wenn die Syntax variieren kann.
Es gibt wichtige Operatoren in der Booleschen Logik:
- AND (
&&oderAND): Beide Bedingungen müssen wahr sein, damit das Ergebnis wahr ist. Beispiele: „Ist die Zahl größer als 5 und kleiner als 10?“ – „Ich gehe spazieren, wenn es schön ist und ich Zeit habe.“ - OR (
||oderOR): Mindestens eine Bedingung muss wahr sein. Beispiele: „Ist die Zahl 5 oder 10?“ – „Ich sehe fern, wenn es regnet oder es ist Wochenende.“ - NOT (
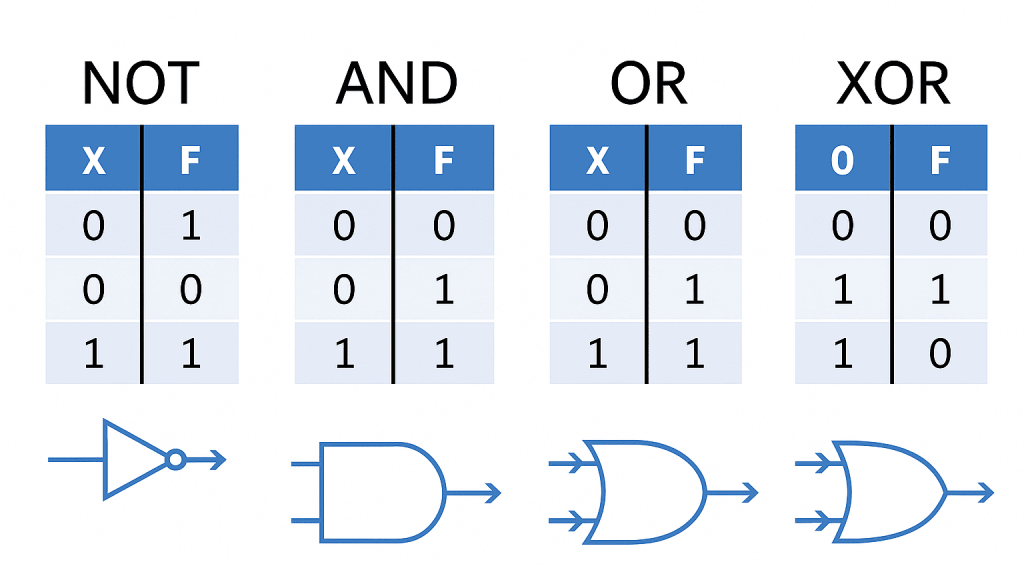
!oderNOT): Negiert eine Bedingung. Beispiele: „Ist die Zahl nicht null?“ – „Ich gehe nur raus, wenn es nicht kalt ist.“ - XOR (Exklusives ODER): Genau eine Bedingung ist wahr, nicht beide. Beispiel: „Entweder Tag oder Nacht, aber nicht beides.“
Verstehst du die Unterschiede? Diese Operatoren ermöglichen es, komplexe Bedingungen im Code zu formulieren. Sie unterscheiden sich in ihrer Bedeutung und Anwendung deutlich.
3. Grundlagen der booleschen Algebra
Boolesche Algebra ist die mathematische Grundlage der Logik. Sie wurde in den 1800er Jahren entwickelt, um logische Zusammenhänge zu erfassen. Für Programmierer ist sie die Basis, um Ausdrücke zu vereinfachen und effizient zu gestalten. Durch die Regeln der Algebra kannst du komplexe Ausdrücke sogar vereinfachen, was den Code schneller macht.
Die Anwendung der booleschen Algebra hilft dabei, redundante Bedingungen zu vermeiden und Fehler zu reduzieren. Sie ist ein Werkzeug, das in fast jeder Programmiersprache genutzt wird.
4. Truth Tables: Das Werkzeug zur Visualisierung logischer Zusammenhänge
4.1. Was sind Truth Tables?
Eine Wahrheitstabelle zeigt dir alle möglichen Wahrheitswerte für deine Variablen. Damit siehst du, wie sich verschiedenen Kombinationen auf das Ergebnis auswirken. Das macht Truth Tables gerade bei komplexen Logik-Ausdrücken unschlagbar.
Der Vorteil? Sie machen Zusammenhänge sichtbar, die im Code schwer zu erkennen sind. So kannst du Fehler schon frühzeitig erkennen und smarter programmieren.
4.2. Aufbau und Erstellung von Truth Tables
Das Erstellen einer Truth Table ist einfach. Du listest alle möglichen Werte deiner Variablen auf. Dann bestimmst du für jede Zeile, was die logische Aussage ergibt. So funktioniert es:
- Bestimme alle Variablen und ihre möglichen Wahrheitswerte.
- Erstelle eine Tabelle, in der alle Kombinationen aufgelistet sind.
- Berechne das Ergebnis für jede Kombination.
4.1.1. UND (AND)
- Bedeutung: Beide Bedingungen müssen
truesein, damit das Ergebnistrueist. - Symbol:
and(Python),&&(C/C++, Java)
Wahrheitstabelle für A AND B:
| A | B | A AND B (A & B) |
|---|---|---|
| true (1) | true (1) | true (1) |
| true (1) | false (0) | false (0) |
| false (0) | true (1) | false (0) |
| false (0) | false (0) | false (0) |
Beispiel:
age = 22
has_id = True
if age >= 18 and has_id:
print("Zugang erlaubt")4.1.2. ODER (OR)
- Bedeutung: Mindestens eine der Bedingungen muss
truesein. - Symbol:
or(Python),||(C/C++, Java)
Wahrheitstabelle für A OR B:
| A | B | A OR B (A || B) |
| true (1) | true (1) | true (1) |
| true (1) | false (0) | true (1) |
| false (0) | true (1) | true (1) |
| false (0) | false (0) | false (0) |
Beispiel:
is_teacher = False
is_admin = True
if is_teacher or is_admin:
print("Zugriff auf Verwaltung erlaubt")4.1.3. NICHT (NOT)
- Bedeutung: Kehrt den Wahrheitswert um.
- Symbol:
not(Python),!(C/C++, Java)
Wahrheitstabelle für NOT A:
| A | NOT A (!A) |
| true (1) | false (0) |
| false (0) | true (1) |
Beispiel:
logged_out = not is_logged_in4.1.4. Exklusives ODER (XOR)
- Bedeutung: Genau eine Bedingung muss
truesein, nicht beide. - Symbol:
^(Python, bitweise)
Wahrheitstabelle für A XOR B:
| A | B | A XOR B (A ^ B) |
| true (1) | true (1) | false (0) |
| true (1) | false (0) | true (1) |
| false (0) | true (1) | true (1) |
| false (0) | false (0) | false (0) |
Beispiel:
a = True
b = False
print(a ^ b)
Ausgabe: True4.2. Aufbau einer Truth Table (Beispiel: (A OR B) AND NOT C)
| A | B | C | NOT C | B AND NOT C | A OR (B AND NOT C) |
| true (1) | true (1) | true (1) | false (0) | false (0) | true (1) |
| true (1) | true (1) | false (0) | true (1) | true (1) | true (1) |
| false (0) | true (1) | false (0) | true (1) | true (1) | true (1) |
| false (0) | false (0) | false (0) | true (1) | false (0) | false (0) |
| false (0) | true (1) | true (1) | false (0) | false (0) | false (0) |
4.3. Optimierung Boolescher Ausdrücke (Vereinfachung)
Mit Hilfe der Booleschen Algebra lassen sich logische Ausdrücke vereinfachen:
Identitäten:
- A AND A = A – A & A = A
- A OR A = A
- A AND TRUE = A
- A AND FALSE = FALSE (0)
- A OR TRUE = TRUE (1)
- A OR FALSE = A
- NOT (NOT A) = A
Beispiel:
# Ursprünglich:
if is_admin and (is_admin or is_teacher):
print("Zugang erlaubt")
# Vereinfachung:
if is_admin:
print("Zugang erlaubt")5. Boolesche Ausdrücke im Code umsetzen
5.1. Konvertierung von Logik in Programmcode
Um einen booleschen Ausdruck im Code zu verwenden, brauchst du die richtige Syntax. In Python sieht das so aus:
if a and b:
# pythonIn Java:
if (a && b) {
// Java
}Bei größeren Ausdrücken ist es wichtig, Klammern richtig zu setzen. So behält man den Überblick.
6. Anwendungsbeispiele aus der Praxis
A. Beispiel 1: Login-Prüfung
def can_access(is_logged_in, role):
return is_logged_in and role == "admin"
print(can_access(True, "admin")) # True
print(can_access(True, "user")) # FalseB. Beispiel 2: Logik für Ampelschaltung
is_red = True
is_green = False
is_yellow = False
if is_red:
print("Stop")
elif is_green:
print("Fahren")
elif is_yellow:
print("Achtung")7. Aufgaben zur Vertiefung
A. Aufgabe 1:
Erstelle eine Wahrheitstabelle für den Ausdruck (A AND B) OR NOT A
Lösung
| A | B | A AND B | NOT A | (A AND B) OR NOT A |
| true (1) | true (1) | true (1) | false (0) | true (1) |
| true (1) | false (0) | false (0) | false (0) | false (0) |
| false (0) | true (1) | false (0) | true (1) | true (1) |
| false (0) | false (0) | false (0) | true (1) | true (1) |
B. Aufgabe 2:
Vereinfache den Ausdruck: (A AND B) OR (A AND NOT B)
Lösung: Verwende das Distributivgesetz:
(A AND B) OR (A AND NOT B) = A AND (B OR NOT B) = A AND TRUE = AC. Aufgabe 3:
Schreibe eine Funktion can_vote(age, has_id), die nur True zurückgibt, wenn die Person mindestens 18 Jahre alt ist und einen Ausweis besitzt.
Lösung: Python
def can_vote(age, has_id):
return age >= 18 and has_id
print(can_vote(20, True)) # True
print(can_vote(17, True)) # False8. Optimierung von logischen Ausdrücken
Nicht jeder Ausdruck ist optimal. Mit Hilfe der booleschen Algebra kannst du oft Vereinfachungen vornehmen. Das spart Rechenzeit und macht den Code verständlicher. Es gibt Tools, die automatische Vereinfachungen vornehmen. Nutze sie, um deinen Code effizienter zu gestalten.
9. Fallstudie: Logik in der echten Softwareentwicklung
Stell dir vor, du entwickelst eine Automatisierung im Smart Home. Du willst, dass die Heizung nur läuft, wenn niemand zuhause ist und die Temperatur zu niedrig ist. Das sind zwei boolesche Bedingungen, die du klug kombinierst.
Bei der Webentwicklung kannst du Zugriffsrechte mit komplexen Logikregeln steuern. Durch Testen und Debuggen mit Truth Tables sorgst du für fehlerfreie Funktionen.
10. Erweiterte Themen und zukünftige Trends
A. Logikgatter in der Hardwareentwicklung
Jeder Computer basiert auf sogenannten Logikgattern – kleine Schaltungen, die den Grundregeln der Booleschen Algebra folgen. Sie bilden die Grundlage für Prozessoren. Mit ihnen lässt sich alles steuern, von einfachen Rechenaufgaben bis zu Künstlicher Intelligenz.
B. Automatisierte Logikgenerierung
Künstliche Intelligenz und maschinelles Lernen helfen heute, logische Regeln automatisch zu entwickeln. Das erleichtert die Programmierung enorm. In Zukunft könnten Entwickler noch schneller komplexe Bedingungen bauen, weil diese Tools viel lernen und optimieren.
11. Herausforderungen und offene Fragen
Die boolesche Logik hat Grenzen. Sie kann nicht alle Entscheidungen abbilden, zum Beispiel Unsicherheiten oder Wahrscheinlichkeiten. Die Weiterentwicklung der Logik-Theorie wird diesen Bereich erweitern. Neue Ansätze könnten die Nutzung in immer komplexeren Systemen ermöglichen.
Fazit
Die Macht der Wahrheit – Logik im Code meistern
Das Verstehen von Truth Tables und boolescher Logik ist für Programmierer fundamental. Es hilft, sichere und effiziente Programme zu schreiben. MitPractically, kannst du komplexe Bedingungen verständlich machen und Fehler vermeiden. Denke immer daran: Gute Logik ist die Basis jeder guten Software. Nutze diese Werkzeuge, um deine Programmierung auf das nächste Level zu heben.
Jetzt ist der perfekte Moment, um deine Bedingungen mit Truth Tables zu prüfen und deine Logik zu verbessern. Starte noch heute und mach deine Programme noch smarter!
Quellen
- Wikipedia: Boolesche Algebra – https://de.wikipedia.org/wiki/Boolesche_Algebra
- Wikipedia: Logikgatter – https://de.wikipedia.org/wiki/Logikgatter
- Khan Academy: Logical Operators (engl.) – https://www.khanacademy.org/computing/computer-science/cryptography/logic/a/logic-operators
- Python Documentation: Boolean Values – https://docs.python.org/3/library/stdtypes.html#boolean-values
- W3Schools: Python Booleans – https://www.w3schools.com/python/python_booleans.asp
- CircuitVerse – https://circuitverse.org (Interaktive Logikgatter)
- Logisim Evolution (Schaltungssimulator) – https://github.com/reds-heig/logisim-evolution